题目内容
19.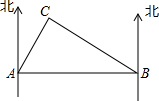 如图,北部湾海面上,一艘解放军军舰在基地A的正东方向且距A地60海里的B处训练,突然接到基地命令,要该舰前往C岛,接送一名病危的渔民到基地医院救治.已知C岛在A的北偏东30°方向,且在B的北偏西60°方向,军舰从B处出发,平均每小时行驶30海里,需要多少时间才能把患病渔民送到基地医院.(精确到0.1小时,$\sqrt{3}$≈1.7)
如图,北部湾海面上,一艘解放军军舰在基地A的正东方向且距A地60海里的B处训练,突然接到基地命令,要该舰前往C岛,接送一名病危的渔民到基地医院救治.已知C岛在A的北偏东30°方向,且在B的北偏西60°方向,军舰从B处出发,平均每小时行驶30海里,需要多少时间才能把患病渔民送到基地医院.(精确到0.1小时,$\sqrt{3}$≈1.7)
分析 根据题意知应求(BC+AC)的长,△ABC为斜三角形,所以需作高转化为直角三角形求解.
解答 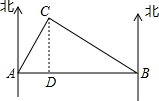 解:根据题意,得∠A=60°,∠B=30°
解:根据题意,得∠A=60°,∠B=30°
作CD⊥AB于D,
设CD=x,∵$\frac{CD}{AD}$=tan60°
∴AD=$\frac{\sqrt{3}}{3}$x
∵$\frac{CD}{BD}$=tan30°
∴BD=$\sqrt{3}$x
∵AB=60,
∴$\sqrt{3}$x+$\frac{\sqrt{3}}{3}$x=60,
解得:x=15$\sqrt{3}$海里,
∴AC=$\frac{2\sqrt{3}}{3}$x=30海里,
BC=2x=30$\sqrt{3}$海里,
∴AC=2x
∴$\frac{AC+BC}{30}$=$\sqrt{3}$+1≈2.7小时,
答:需要大约2.7小时才能把患病渔民送到基地医院.
点评 考查了勾股定理及解直角三角形的应用,“化斜为直”是解三角形的常规思路,常需作垂线(或高).原则上不破坏特殊角(30°、45°、60°).

练习册系列答案
相关题目
9.绵阳到某地相距n千米,提速前火车从绵阳到某地要t小时,提速后行车时间减少了0.5小时,提速后火车的速度比原来速度快了( )
| A. | $\frac{n}{t-0.5}$ | B. | $\frac{n}{t}$ | C. | $\frac{n}{t-0.5}$-$\frac{n}{t}$ | D. | $\frac{n}{t}$-$\frac{n}{t-0.5}$ |
11.已知|3a-2b-12|+(a+2b+4)2=0.则( )
| A. | $\left\{\begin{array}{l}{a=0}\\{b=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=2}\\{b=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-3}\\{b=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=-2}\\{b=-3}\end{array}\right.$ |
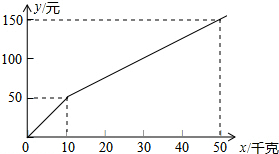 某种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格打折,因此付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如果所示,下列四种说法:
某种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格打折,因此付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如果所示,下列四种说法: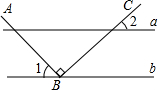 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=44°,求∠2的度数.
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=44°,求∠2的度数.