ΧβΡΩΡΎ»ί
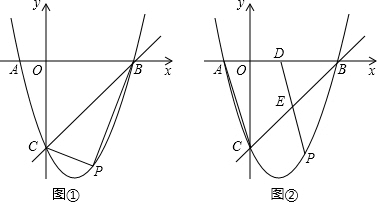
»γΆΦΔΌΘ°÷±œΏy=x-3”κx÷αΓΔy÷αΖ÷±πΫΜ”ΎBΓΔCΝΫΒψΘ§ΒψA‘Ύx÷αΗΚΑκ÷α…œΘ§«“
=
Θ°≈ΉΈοœΏΨ≠ΙΐAΓΔBΓΔC»ΐΒψΘ§ΒψPΘ®mΘ§nΘ© «ΗΟ≈ΉΈοœΏ…œΒΡ“ΜΗωΕ·ΒψΘ®Τδ÷–mΘΨ0Θ§nΘΦ0Θ©Θ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©Ν§Ϋ”PCΓΔPBΘ®»γΆΦΔΌΘ©Θ§ΓςPBC «Ζώ”–Ήν¥σΟφΜΐΘΩ»τ”–Θ§«σ≥ωΓςPBCΒΡΉν¥σΟφΜΐΚΆ¥Υ ±PΒψΒΡΉχ±ξΘΜ»τΟΜ”–Θ§«κΥΒΟςάμ”…ΘΜ
Θ®3Θ©DΈΣœΏΕΈAB÷–ΒψΘ§Ν§ΫαDPΫΜBC”ΎΒψEΘ°Ν§ΫαACΘ®»γΆΦΔΎΘ©Θ§»τ“‘BΘ§DΘ§EΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςABCœύΥΤΘ°÷±Ϋ”–¥≥ω¥Υ ±ΒψPΒΡΉχ±ξΘ°
| OA |
| OC |
| 1 |
| 3 |
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©Ν§Ϋ”PCΓΔPBΘ®»γΆΦΔΌΘ©Θ§ΓςPBC «Ζώ”–Ήν¥σΟφΜΐΘΩ»τ”–Θ§«σ≥ωΓςPBCΒΡΉν¥σΟφΜΐΚΆ¥Υ ±PΒψΒΡΉχ±ξΘΜ»τΟΜ”–Θ§«κΥΒΟςάμ”…ΘΜ
Θ®3Θ©DΈΣœΏΕΈAB÷–ΒψΘ§Ν§ΫαDPΫΜBC”ΎΒψEΘ°Ν§ΫαACΘ®»γΆΦΔΎΘ©Θ§»τ“‘BΘ§DΘ§EΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςABCœύΥΤΘ°÷±Ϋ”–¥≥ω¥Υ ±ΒψPΒΡΉχ±ξΘ°

ΩΦΒψΘΚΕΰ¥ΈΚ· ΐΉέΚœΧβ
Ή®ΧβΘΚ
Ζ÷ΈωΘΚΘ®1Θ©άϊ”ΟΫΜΒψ Ϋ«σ≥ωΕΰ¥ΈΚ· ΐΫβΈω ΫΦ¥Ω…ΘΜ
Θ®2Θ©«σ≥ωΓςPBCΒΡΉν¥σΟφΜΐΘ§Ω…“‘ΝΣœΒΕΰ¥ΈΚ· ΐΒΡΉν÷ΒΈ ΧβΘ§Ζ÷ΗνΆΦ–Έ«σ≥ωΦ¥Ω…ΘΜ
Θ®3Θ©άϊ”ΟΔΌΒ±DEΓΈACΘ§‘ρΓςBDEΓΉΓςBACΘ§ΔΎΒ±ΓœBED=ΓœBACΘ§ΓςBDEΓΉΓςBCAΘ§ΫχΕχ«σ≥ωPΒψΉχ±ξΘ°
Θ®2Θ©«σ≥ωΓςPBCΒΡΉν¥σΟφΜΐΘ§Ω…“‘ΝΣœΒΕΰ¥ΈΚ· ΐΒΡΉν÷ΒΈ ΧβΘ§Ζ÷ΗνΆΦ–Έ«σ≥ωΦ¥Ω…ΘΜ
Θ®3Θ©άϊ”ΟΔΌΒ±DEΓΈACΘ§‘ρΓςBDEΓΉΓςBACΘ§ΔΎΒ±ΓœBED=ΓœBACΘ§ΓςBDEΓΉΓςBCAΘ§ΫχΕχ«σ≥ωPΒψΉχ±ξΘ°
Ϋβ¥πΘΚΫβΘΚΘ®1Θ©AΘ®-1Θ§0Θ©Θ§BΘ®3Θ§0Θ©Θ§CΘ®0Θ§-3Θ©
…η≈ΉΈοœΏΫβΈω ΫΈΣy=aΘ®x+1Θ©Θ®x-3Θ©Θ§Α―CΘ®0Θ§-3Θ©¥ζ»κΒΟ-3a=-3Θ§
ΫβΒΟa=1Θ°
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=x2-2x-3Θ°
Θ®2Θ©»γΆΦΔΌΥυ ΨΘΚ
ΉςPFΓΆx÷α”ΎΒψFΘ§…ηΓςPBCΒΡΟφΜΐΈΣSΘ§‘ρ
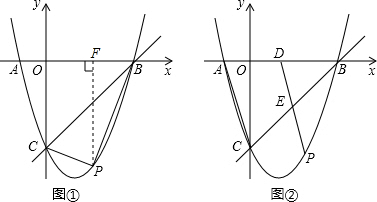
S=SΥΡ±Ώ–ΈOCPF+SΓςPFB-SΓςOBC
=
Θ®3-nΘ©m+
Θ®3-mΘ©Θ®-nΘ©-
ΓΝ3ΓΝ3Θ§
=
m-
n-
Θ§
”÷ΓΏΒψP «≈ΉΈοœΏ…œΒΡΒψΘ§
«“mΘΨ0Θ§nΘΦ0
Γύn=m2-2m-3Θ®0ΘΦmΘΦ3Θ©
ΓύS=-
m2+
m
=-
Θ®m-
Θ©2+
ΓύΒ±m=
±Θ§ΓςPBCΒΡΟφΜΐΉν¥σΘ§Ήν¥σΟφΜΐΈΣ
Θ§
Α―x=m=
¥ζ»κy=x2-2x-3=Θ®
Θ©2-2ΓΝ
-3=-
Θ§
¥Υ ±PΒψΉχ±ξΈΣΘ®
Θ§-
Θ©ΘΜ
Θ®3Θ©Ζ÷ΝΫ÷÷«ιΩωΘΚ
ļ±DEøACȧ
ΓύΓςBDEΓΉΓςBACΘ§
Γύ
=
Θ§
ΓΏDΈΣAB÷–ΒψΘ§
ΓύEΒψΈΣBC÷–ΒψΘ§
ΓύEΘ®
Θ§-
Θ©
Γύ…ηDEΥυ‘ΎΫβΈω ΫΈΣΘΚy=kx+bΘ§
Γύ
Θ§
ΫβΒΟΘΚ
Θ§
ΓύDEΥυ‘ΎΫβΈω ΫΈΣΘΚy=-3x+3Θ§
‘ρ-3x+3=x2-2x-3Θ§
ΫβΒΟΘΚx1=2Θ§x2=-3Θ®≤ΜΚœΧβ“β…α»ΞΘ©Θ§
ΓύP1Θ®2Θ§-3Θ©ΘΜ
ΔΎΒ±ΓœBED=ΓœBACΘ§
ΓύΓςBDEΓΉΓςBCAΘ§
Ά§άμΩ…ΒΟ≥ωΘΚP2Θ®
Θ§2-2
Θ©Θ§
Ήέ…œΥυ ωΘΚPΒψΉχ±ξΈΣΘΚΘ®2Θ§-3Θ©Θ§Θ®
Θ§2-2
Θ©Θ°
…η≈ΉΈοœΏΫβΈω ΫΈΣy=aΘ®x+1Θ©Θ®x-3Θ©Θ§Α―CΘ®0Θ§-3Θ©¥ζ»κΒΟ-3a=-3Θ§
ΫβΒΟa=1Θ°
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=x2-2x-3Θ°
Θ®2Θ©»γΆΦΔΌΥυ ΨΘΚ
ΉςPFΓΆx÷α”ΎΒψFΘ§…ηΓςPBCΒΡΟφΜΐΈΣSΘ§‘ρ
S=SΥΡ±Ώ–ΈOCPF+SΓςPFB-SΓςOBC
=

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
”÷ΓΏΒψP «≈ΉΈοœΏ…œΒΡΒψΘ§
«“mΘΨ0Θ§nΘΦ0
Γύn=m2-2m-3Θ®0ΘΦmΘΦ3Θ©
ΓύS=-
| 3 |
| 2 |
| 9 |
| 2 |
=-
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
ΓύΒ±m=
| 3 |
| 2 |
| 27 |
| 8 |
Α―x=m=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 15 |
| 4 |
¥Υ ±PΒψΉχ±ξΈΣΘ®
| 3 |
| 2 |
| 15 |
| 4 |
Θ®3Θ©Ζ÷ΝΫ÷÷«ιΩωΘΚ
ļ±DEøACȧ
ΓύΓςBDEΓΉΓςBACΘ§
Γύ
| BD |
| AB |
| BE |
| EC |
ΓΏDΈΣAB÷–ΒψΘ§
ΓύEΒψΈΣBC÷–ΒψΘ§
ΓύEΘ®
| 3 |
| 2 |
| 3 |
| 2 |
Γύ…ηDEΥυ‘ΎΫβΈω ΫΈΣΘΚy=kx+bΘ§
Γύ
|
ΫβΒΟΘΚ
|
ΓύDEΥυ‘ΎΫβΈω ΫΈΣΘΚy=-3x+3Θ§
‘ρ-3x+3=x2-2x-3Θ§
ΫβΒΟΘΚx1=2Θ§x2=-3Θ®≤ΜΚœΧβ“β…α»ΞΘ©Θ§
ΓύP1Θ®2Θ§-3Θ©ΘΜ
ΔΎΒ±ΓœBED=ΓœBACΘ§
ΓύΓςBDEΓΉΓςBCAΘ§
Ά§άμΩ…ΒΟ≥ωΘΚP2Θ®
| 5 |
| 5 |
Ήέ…œΥυ ωΘΚPΒψΉχ±ξΈΣΘΚΘ®2Θ§-3Θ©Θ§Θ®
| 5 |
| 5 |
ΒψΤάΘΚ¥ΥΧβ÷ς“ΣΩΦ≤ιΝΥ”Ο¥ΐΕ®œΒ ΐΖ®«σΕΰ¥ΈΚ· ΐΫβΈω ΫΘ§“‘ΦΑΕΰ¥ΈΚ· ΐΉν÷ΒΈ ΧβΘ§άϊ”ΟΖ÷άύΧ÷¬έΒΟ≥ω «ΫβΧβΙΊΦϋΘ§ΉέΚœ–‘±»Ϋœ«ΩΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
“―÷ΣΘΚ“Μ‘ΣΕΰ¥ΈΖΫ≥Χx2-4x+2=0ΒΡΝΫΗυΈΣx1ΓΔx2Θ§‘ρx1+x2-x1x2ΒΡ÷ΒΈΣΘ®ΓΓΓΓΘ©
| AΓΔ-6 | BΓΔ6 | CΓΔ2 | DΓΔ-2 |
 »γΆΦΘ§ΓςABDΘ§ΓςAECΕΦ «Β»±Ώ»ΐΫ«–ΈΘ§
»γΆΦΘ§ΓςABDΘ§ΓςAECΕΦ «Β»±Ώ»ΐΫ«–ΈΘ§
 »γΆΦΘ§BΘ§EΘ§CΘ§FΥΡΒψ‘Ύ“ΜΧθ÷±œΏ…œΘ§AB=DEΘ§BE=CFΘ§ΓœB=ΓœDEFΘ°«σ÷ΛΘΚACΓΈDFΘ°
»γΆΦΘ§BΘ§EΘ§CΘ§FΥΡΒψ‘Ύ“ΜΧθ÷±œΏ…œΘ§AB=DEΘ§BE=CFΘ§ΓœB=ΓœDEFΘ°«σ÷ΛΘΚACΓΈDFΘ° »γΆΦΘ§‘ΎΧί–ΈABCD÷–Θ§ABΓΈCDΘ§ΓœDAB=90ΓψΘ§ACΓΆBCΘ°
»γΆΦΘ§‘ΎΧί–ΈABCD÷–Θ§ABΓΈCDΘ§ΓœDAB=90ΓψΘ§ACΓΆBCΘ°