题目内容
11.小兵在用长度为10cm,45cm和50cm的三根木条钉一个三角形,不小心将50cm的一根折断了,之后就怎么也钉不成一个三角形木架.(1)最长的木条至少折断了多少厘米?
(2)如果最长的木条折断了25cm,你怎样通过截木条的方法钉成一个小三角形?
分析 (1)根据三角形的三边关系:三角形两边之和大于第三边.三角形的两边差小于第三边求解即可;
(2)根据三边关系确定第三边的长,然后确定折去的木条的长度即可.
解答 解:(1)∵两根木条的长为10cm、45cm,
∴若第三根木条的长x满足45-10<x<45+10,
即:35<x<55,
∵第三根木条为50cm,
50-35=15cm,
∴最长的木条至少折断了15厘米;
(2)如果折去了25cm,则还剩25cm,要想钉成一个三角形架可以将45cm长的木条折去大于10cm小于30cm的一部分.
点评 本题考查了三角形三边关系,解题的关键是确定第三边的取值范围,难度不大.

练习册系列答案
相关题目
1.多项式x2+3x-2中,下列说法错误的是( )
| A. | 这是一个二次三项式 | B. | 二次项系数是1 | ||
| C. | 一次项系数是3 | D. | 常数项是2 |
6.计算4$\sqrt{6{x}^{3}}$÷2$\sqrt{\frac{x}{3}}$的结果为( )
| A. | 2$\sqrt{2}x$ | B. | $\frac{2x}{3}$ | C. | 6$\sqrt{2}x$ | D. | $\frac{2\sqrt{2}}{3}$x |
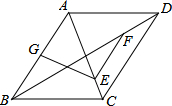 如图,在平行四边形ABCD中,BD=2AD,点E、F、G分别为OC、OD、AB的中点,求证:EF=EG.
如图,在平行四边形ABCD中,BD=2AD,点E、F、G分别为OC、OD、AB的中点,求证:EF=EG.