题目内容
7. 为纪念京汉铁路工人大罢工而修建的二七纪念塔于去年下半年重新整修,一装修工人站在塔的顶部处测得对面一栋AB=9米高的楼房的俯角为45°,测得楼房正前方18.2米处一站牌底部C点的俯角为60°,请你帮助装修工人计算塔的高度是多少?(已知装修工人身高为1.8米,眼部到头顶的距离和塔身的宽度都忽略不计,$\sqrt{3}$≈1.732,结果保留到1米)
为纪念京汉铁路工人大罢工而修建的二七纪念塔于去年下半年重新整修,一装修工人站在塔的顶部处测得对面一栋AB=9米高的楼房的俯角为45°,测得楼房正前方18.2米处一站牌底部C点的俯角为60°,请你帮助装修工人计算塔的高度是多少?(已知装修工人身高为1.8米,眼部到头顶的距离和塔身的宽度都忽略不计,$\sqrt{3}$≈1.732,结果保留到1米)
分析 作AF⊥DE于F,根据题意得出FE=AB=9米,AF=BE,∠DAF=45°,∠DCE=60°,设CE=x米,解直角三角形得出DE=$\sqrt{3}$CE=$\sqrt{3}$x(米),AF=DF,因此DF=DE-FE=$\sqrt{3}$x-9(米),得出方程,解方程即可18.2+x=$\sqrt{3}$x-9,求出CE,得出DE,即可得出结果.
解答 解:如图所示: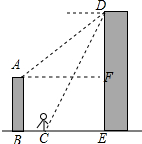 作AF⊥DE于F,
作AF⊥DE于F,
根据题意得:FE=AB=9米,BC=18.2米,AF=BE,∠DAF=45°,∠DCE=60°,
设CE=x米,
∵∠DEC=90°,∠DCE=60°,
∴DE=$\sqrt{3}$CE=$\sqrt{3}$x(米),
∴DF=DE-FE=$\sqrt{3}$x-9(米),
∵∠AFD=90°,∠DAF=45°,
∴AF=DF,
即18.2+x=$\sqrt{3}$x-9,
解得:x≈37.16(米),
∴DE=$\sqrt{3}$x≈64.36(米),
∴塔的高度为64.36-1.8≈63(米);
答:塔的高度约为63米.
点评 本题考查解直角三角形的应用-仰角俯角问题,要求学生能借助仰角俯角构造直角三角形并解直角三角形,根据题意得出方程是解决问题的关键.

练习册系列答案
相关题目
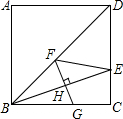 如图,正方形ABCD中,连接BD,在DC上取一点E,在BD上取一点F,使得∠BEC=∠DEF,过点F作FG⊥BE于H,交BC于G,若DE=5$\sqrt{6}$,GC=7,则CE=5$\sqrt{6}$-7.
如图,正方形ABCD中,连接BD,在DC上取一点E,在BD上取一点F,使得∠BEC=∠DEF,过点F作FG⊥BE于H,交BC于G,若DE=5$\sqrt{6}$,GC=7,则CE=5$\sqrt{6}$-7.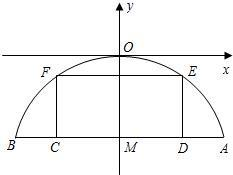 有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为9米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.
有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为9米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.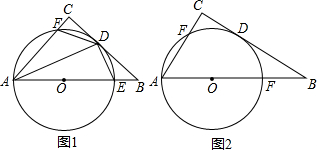
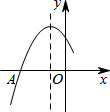 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论: