题目内容
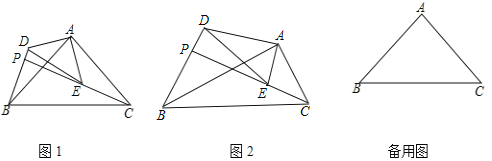
【题目】如图，
和
是有公共顶点的直角三角形，
，点P为射线BD，CE的交点．
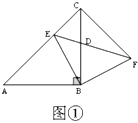
（1）如图1，若和是等腰三角形，求证：
；
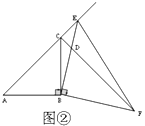
（2）如图2，若
，问：（1）中的结论是否成立？请说明理由．
（3）在（1）的条件下，若
，
，若把绕点A旋转，当
时，求PB的长．
【答案】（1）证明见解析；（2）成立，理由见解析；（3）
或
．
【解析】
（1）由题意依据等腰三角形的性质得到
，
，依据同角的余角相等得到
，然后依据SAS可证明
≌
，最后，依据全等三角形的性质可得到
；
（2）根据题意先判断出∽，进行分析即可得出结论；
（3）由题意分为点E在AB上和点E在AB的延长线上两种情况画出图形，然后再证明
∽，最后依据相似三角形的性质进行证明即可．
解：（1）
和
是等腰直角三角形，
，
，
，．
≌．
．
（2）（1）中结论成立，理由：
在
中，
，
，
在
中，
，
，
，
，
∽，
.
（3）解：
当点E在AB上时，
．
，
．
同（1）可证≌．
，
，
∽．
，
，
．
当点E在BA延长线上时，
．
，
，
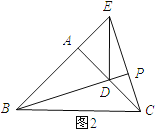
同（1）可证≌．
，
，
∽．
，
，
．
综上所述，PB的长为
或
．
练习册系列答案
相关题目
