题目内容
【题目】如图,已知![]() ,点
,点![]() 为直线
为直线![]() 上一点,以
上一点,以![]() 为边,点
为边,点![]() 为直角顶点作等腰直角三角形
为直角顶点作等腰直角三角形![]() .
.
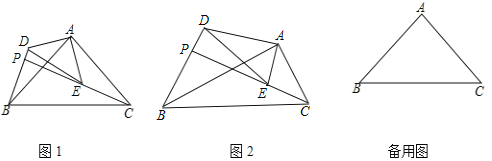
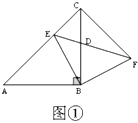
(1)如图①,当点![]() 在线段
在线段![]() 上时,
上时,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ;
;
①找出一对全等三角形为_____________;
②若四边形![]() 的面积为7,则
的面积为7,则![]() 的长是_______.
的长是_______.
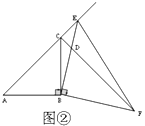
(2)如图②,当点![]() 在
在![]() 的延长线上时,
的延长线上时,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
①![]() 的面积记为
的面积记为![]() ,
,![]() 的面积记为
的面积记为![]() ,探究
,探究![]() 、
、![]() 之间的数量关系并说明理由;
之间的数量关系并说明理由;
②当![]() 的面积为1时,求
的面积为1时,求![]() 的长.
的长.
【答案】(1)①![]() ;②3;(2)①
;②3;(2)①![]() ,理由见解析;②
,理由见解析;②![]()
【解析】
(1)①由“SAS”可证△ABE≌△CBF;
②过点B作BM⊥AC于M,由三角形的面积公式可求S△ABC=![]() ×4×2=4,可求S△CBF=3=S△ABM,即可求AE的长;
×4×2=4,可求S△CBF=3=S△ABM,即可求AE的长;
(2)①由全等三角形的性质S△ABE=S△CBF,由三角形面积关系可求4+m=n;
②过点B作BG⊥AC,BH⊥FC,由全等三角形的性质可得AE=CF,∠A=∠BCH=45°=∠ACB,由角平分线的性质可得BG=BH=2,由三角形面积可求DF=5,设AE=x,则![]() ,由三角形面积公式可列出
,由三角形面积公式可列出![]() ,可求x的值,即可得AE的长.
,可求x的值,即可得AE的长.
解:(1)①△ABE≌△CBF;
理由如下:
∵∠ABC=∠EBF=90°,
∴∠ABE=∠CBF,且AC=BC,EB=BF
∴△ABE≌△CBF(SAS)
故答案为:△ABE≌△CBF;
②如图,过点B作BM⊥AC于M,
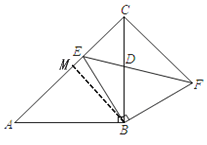
∵∠ABC=90°,AB=BC,AC=4,BM⊥AC,
∴AM=CM=BM=2
∴S△ABC=![]() ×4×2=4
×4×2=4
∵S四边形ABFC=7
∴S△CBF=3=S△ABM,
∴![]() ×AE×BM=3
×AE×BM=3
∴AE=3
故答案为:3;
(2)①∵![]()
∴![]()
即![]()
∴![]()
∴![]()
②由①得:![]()
当![]() 时,
时,![]()
即![]() ,
,![]()
过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,
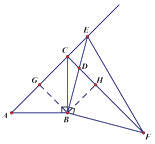
在![]() 中∵
中∵![]() ,
,
∴![]()
∵![]()
∴![]()
∴![]()
即![]() 平分
平分![]() ,且
,且![]() ,
,![]()
∴![]()
∵![]()
∴![]()
即![]()
则![]()
设![]() ,则
,则![]() ,
,![]() ,
,![]()
∵![]()
∴![]()
即![]()
∵![]()
∴![]()
即![]()
化简得:![]()
解得:![]() (不合题意,舍去)
(不合题意,舍去)
即![]() .
.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目