题目内容
4. 如图,在△ABC中,D、E分别是AB和AC上的点,且DE∥BC.
如图,在△ABC中,D、E分别是AB和AC上的点,且DE∥BC.(1)若AD=5,DB=7,EC=12,求AE的长.
(2)若AB=16,AD=4,AE=8,求EC的长.
分析 (1)根据平行线分线段成比例,可以求得AE的长;
(2)根据平行线分线段成比例,可以求得AC的长,从而可以求得EC的长.
解答 解:(1)∵DE∥BC,
∴$\frac{AD}{DB}=\frac{AE}{EC}$,
∵AD=5,DB=7,EC=12,
∴$\frac{5}{7}=\frac{AE}{12}$,
解得,AE=$\frac{60}{7}$;
(2))∵DE∥BC,
∴$\frac{AD}{AB}=\frac{AE}{AC}$,
∵AB=16,AD=4,AE=8,
∴$\frac{4}{16}=\frac{8}{AC}$,
解得,AC=32,
∴EC=AC-AE=32-8=24.
点评 本题考查平行线分线段成比例,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
 如图,在△ABC中,AC的垂直平分线交BC于D,垂足为E,△ABD的周长为13cm,AC=5cm,求△ABC的周长.
如图,在△ABC中,AC的垂直平分线交BC于D,垂足为E,△ABD的周长为13cm,AC=5cm,求△ABC的周长.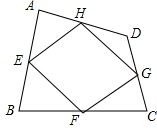 已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形). 把下列各数0,(-2)2,-|-4|,-$\frac{3}{2}$,-(-1)在数轴上表示出来,并用“<”号把这些数连接起来.
把下列各数0,(-2)2,-|-4|,-$\frac{3}{2}$,-(-1)在数轴上表示出来,并用“<”号把这些数连接起来.