题目内容
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标(4,2),过点D(0,3)和E(6,0)的直线分别于AB,BC交于点M,N.
 (1)求直线DE的解析式和点M的坐标;
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数y=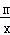 (x>0)的图象经过点M,
(x>0)的图象经过点M,
求该反比函数的解析式,并通过计算判断点
N是否在该函数的图象上.
解:(1)设直线DE的解析式为y=kx+b,
∵D(0,3),E(6,0),
∴ ,解得
,解得 , ∴直线DE的解析式为y=﹣
, ∴直线DE的解析式为y=﹣ x+3;
x+3;
当y=2时,﹣ x+3=2,解得x=2, ∴M的坐标为(2,2);
x+3=2,解得x=2, ∴M的坐标为(2,2);
(2)∵反比例函数y= (x>0)的图象经过点M(2,2),
(x>0)的图象经过点M(2,2),
∴m=2×2=4, ∴该反比函数的解析式是y= ;
;
∵直线DE的解析式为y=﹣ x+3, ∴当x=4时,y=﹣
x+3, ∴当x=4时,y=﹣ ×4+3=1, ∴N点坐标为(4,1),
×4+3=1, ∴N点坐标为(4,1),
∵4×1=4, ∴点N在函数y= 的图象上.
的图象上.
点评: 本题考查了反比例函数与一次函数的交点问题,矩形的性质,待定系数法求一次函数与反比例函数的解析式,反比例函数与一次函数图象上点的坐标特征,难度适中.正确求出两函数的解析式是解题的关键.

 字词句段篇系列答案
字词句段篇系列答案李华根据演讲比赛中九位评委所给的分数制作了如下表格:
| 平均数 | 中位数 | 众数 | 方差 |
| 8.5 | 8.3 | 8.1 | 0.15 |
如果要去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
A.平均数 B. 众数 C. 方差 D.中位数
兰新铁路的通车,圆了全国人民的一个梦,坐上火车去观赏青海门源百里油菜花海,感受大美青海独特的高原风光,暑假某校准备组织学生、老师到门源进行社会实践,为了便于管理,师生必须乘坐在同一列高铁上,根据报名人数,若都 买一等座单程火车票需2340元,若都买二等座单程火车票花钱最少,则需1650元:
买一等座单程火车票需2340元,若都买二等座单程火车票花钱最少,则需1650元:
西宁到门源的火车票价格如下表
| 运行区间 | 票价 | ||
| 上车站 | 下车站 | 一等座 | 二等座 |
| 西宁 | 门源 | 36元 | 30元 |
(1)参加社会实践的学生、老师各有多少人?
(2)由于各种原因,二等座火车票单程只能买x张(参加社会实践的学生人数<x<参加社会实践的总人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐并且总费用最低的前提下,请你写出购买火车票的总费用(单程)y与x之间的函数关系式.

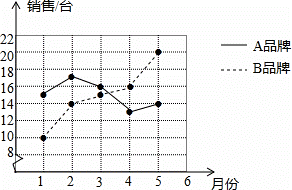
 据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性.
据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性. ,则图中阴影部分的面积是( )
,则图中阴影部分的面积是( )
 ﹣
﹣ B.
B.  C.
C.  ﹣
﹣ )2+
)2+ ﹣2sin45°﹣|1﹣
﹣2sin45°﹣|1﹣ |.
|.
 B.
B. C.
C. D.
D.
 ,则阴影部分的面积为 .
,则阴影部分的面积为 .