题目内容
4.口袋中有4个分别写着字母A、B、C、D的小球,这些小球除字母外都相同,现在随机抽取一个小球后放回,再随机抽取一个小球.(1)用画树状的方法表示所有可能的结果;
(2)求两次取得相同字母的概率.
分析 (1)利用树状图可展示所有16种等可能的计算数;
(2)在所有结果数中找出两次取得相同字母的结果数,然后根据概率公式求解.
解答 解:(1)画树状图为:
共有16种等可能的结果数;
(2)两次取得相同字母的结果数为4,
所以两次取得相同字母的概率=$\frac{4}{16}$=$\frac{1}{4}$.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.

练习册系列答案
相关题目
14.一次函数的一般形式是(k、b是常数)( )
| A. | y=kx+b | B. | y=kx | C. | y=kx+b(k≠0) | D. | y=x |
19.下列计算正确的是( )
| A. | -1+2=-3 | B. | -1-1=0 | C. | 0-2=2 | D. | -2-(-5)=3 |
13.南昌市某路公交车共有10站,我们把上客人数记为“+”,把下客人数记为“-”,一次该路一辆公交车各站上、下人数列表如下:
(1)求表格中x的值;
(2)求在⑤、⑥站之间该公交车上的人数;
(3)问在哪两站之间,该公交车上的人数最多?并求最多人数.
| ①始发站 | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩终点站 | |
| 上客人数 | 9 | 8 | 10 | 12 | 14 | 13 | 11 | 6 | 7 | 0 |
| 下客人数 | 0 | -3 | -5 | -7 | -4 | -8 | -6 | -9 | x | -28 |
(2)求在⑤、⑥站之间该公交车上的人数;
(3)问在哪两站之间,该公交车上的人数最多?并求最多人数.
 如图,△ABC中,BD平分∠ABC,∠ABC=60°,∠C=40°,求∠ADB的度数.
如图,△ABC中,BD平分∠ABC,∠ABC=60°,∠C=40°,求∠ADB的度数.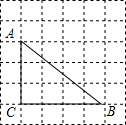 如图,正方形网格的每一个小正方形的边长都为1,△ABC的三个顶点都在正方形的顶点上,完成下面问题:
如图,正方形网格的每一个小正方形的边长都为1,△ABC的三个顶点都在正方形的顶点上,完成下面问题: