题目内容
6.解下列方程:(1)3x2+4x-6=0;
(2)(x-4)(x-2)=24.
分析 (1)利用配方法求出方程的解即可;
(2)首先去括号,然后合并同类项,再利用因式分解法求出方程的解即可.
解答 解:(1)∵3x2+4x-6=0,
∴3(x2+$\frac{4}{3}$x+$\frac{4}{9}$-$\frac{4}{9}$-2)=0,
∴3(x+$\frac{2}{3}$)2=$\frac{22}{3}$,
∴x+$\frac{2}{3}$=±$\frac{\sqrt{22}}{3}$,
∴x1=$\frac{\sqrt{22}-2}{3}$,x2=$\frac{-\sqrt{22}-2}{3}$;
(2)∵(x-4)(x-2)=24,
∴x2-6x-16=0,
(x-8)(x+2)=0,
∴x-8=0或x+2=0,
∴x1=8,x2=-2.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
相关题目
16.在某地举行的世界博览会总投资约450亿元人民币,其中“450亿”用科学记数法表示为( )
| A. | 4.5×1010 | B. | 4.5×109 | C. | 4.5×108 | D. | 0.45×109 |
11.以下列各组线段为边,能组成三角形的是( )
| A. | 2cm,3cm,5cm | B. | 3cm,3cm,6cm | C. | 5cm,8cm,2cm | D. | 4cm,5cm,6cm |
18. 二次函数y=ax2+bx+c的部分对应值如下表:
二次函数y=ax2+bx+c的部分对应值如下表:
(1)求二次函数的解析式;
(2)直接写出二次函数的对称轴x=1,顶点坐标(1,-9),与x轴的交点(-2,0)、(4,0),与y轴的交点(0,-8);
(3)画出这个二次函数的图象,利用图象直接写出当x为何值时,y>0.
 二次函数y=ax2+bx+c的部分对应值如下表:
二次函数y=ax2+bx+c的部分对应值如下表:| x | … | -3 | -2 | 0 | 1 | 3 | 4 | 5 | … |
| y | … | 7 | 0 | -8 | -9 | -5 | 0 | 7 | … |
(2)直接写出二次函数的对称轴x=1,顶点坐标(1,-9),与x轴的交点(-2,0)、(4,0),与y轴的交点(0,-8);
(3)画出这个二次函数的图象,利用图象直接写出当x为何值时,y>0.
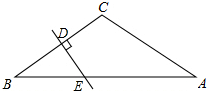 如图,在等腰△ABC中,∠BCA=120°,DE是AC的垂直平分线,线段DE=1cm,求BE的长.
如图,在等腰△ABC中,∠BCA=120°,DE是AC的垂直平分线,线段DE=1cm,求BE的长.