题目内容
5.小明和小红一起做作业,在解一道一元二次方程时,小明在化简过程中写错了常数项,因而得到方程的两个根是8和2;小红在化简过程中写错了一次项的系数,因而得到方程的两个根是-9和-1,你知道原来的方程是什么吗?分析 先设这个方程的两根是α、β,根据两个根是8和2和两个根是-9和-1,得出α+β=-$\frac{b}{a}$=10,αβ=$\frac{c}{a}$=9,从而得出符合题意的方程.
解答 解:设此方程的两个根是α、β,根据题意得:
α+β=-$\frac{b}{a}$=10,αβ=$\frac{c}{a}$=9,
则以α、β为根的一元二次方程是x2-10x+9=0.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.计算a6(a2)3的结果等于( )
| A. | a11 | B. | a12 | C. | a14 | D. | a36 |
16.某自行车计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天产量与计划量相比有出入.下表是某周的生产情况(超产记为正、减产记为负):
(1)根据记录的数据可知该厂星期四生产自行车213辆;
(2)根据记录的数据可知该厂本周实际生产自行车1409辆;
(3)该厂实行每周计件工资制,每生产一辆可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣20元,那么该厂工人这一周的工资总额是多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
(2)根据记录的数据可知该厂本周实际生产自行车1409辆;
(3)该厂实行每周计件工资制,每生产一辆可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣20元,那么该厂工人这一周的工资总额是多少?
20.用配方法解方程x2+8x+9=0,变形后的结果正确的是( )
| A. | (x+4)2=-7 | B. | (x+4)2=-9 | C. | (x+4)2=7 | D. | (x+4)2=25 |
10.二次根式$\sqrt{{a}^{2}}$=-a的条件是( )
| A. | a>0 | B. | a<0 | C. | a≤0 | D. | a是任意实数 |
17.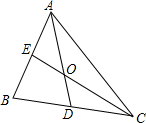 如图,在△ABC中,点O是其重心,连接AO,CO并延长,分别交BC,AB于D,E两点,则下列说法中一定正确的是( )
如图,在△ABC中,点O是其重心,连接AO,CO并延长,分别交BC,AB于D,E两点,则下列说法中一定正确的是( )
 如图,在△ABC中,点O是其重心,连接AO,CO并延长,分别交BC,AB于D,E两点,则下列说法中一定正确的是( )
如图,在△ABC中,点O是其重心,连接AO,CO并延长,分别交BC,AB于D,E两点,则下列说法中一定正确的是( )| A. | ∠BAD=∠CAD | B. | AE=CD | C. | OA=OC | D. | BD=CD |
14.将面积为a2的正方形边长增加2,则正方形的面积增加了( )
| A. | 4 | B. | 2a+4 | C. | 4a+4 | D. | 4a |