题目内容
已知等腰三角形的腰长为10，底边长12，则底边上的高是（ ）
| A、6 | B、8 | C、10 | D、12 |
考点：勾股定理,等腰三角形的性质
专题：
分析：根据题意画出图形，先根据等腰三角形的性质求出BD的长，再根据勾股定理求出AD的长即可．
解答：
解：如图所示，
∵AB=AC=10，BC=12，AD⊥BC，
∴BD=
BC=6，
∴AD=
=
=8．
故选B．
解：如图所示，∵AB=AC=10，BC=12，AD⊥BC，
∴BD=
| 1 |
| 2 |
∴AD=
| AB2-BD2 |
| 102-62 |
故选B．
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，晚上小亮在路灯下经过，在小亮由A处径直走到B处这一过程中，他在地上的影子（ ）| A、逐渐变短 |
| B、先变短后变长 |
| C、逐渐变长 |
| D、先变长后变短 |
已知一个几何体的三视图如图所示，描述该几何体的形状，并根据图上标记的数据求出它的侧面积．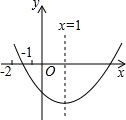
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：