题目内容
12.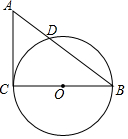 如图,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O,交AB于点D.
如图,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O,交AB于点D.(1)求线段AD的长度;
(2)E是线段AC上一动点,试问当点E运动到什么位置时,直线ED与⊙O相切,请写出你的思路.
分析 (1)首先连接CD,由BC为直径,可得∠BDC=90°,然后由勾股定理求得AB的长,再利用等积法,求得答案;
(2)由ED与⊙O相切,得∠EDO=ECO=90°,又由ED,EC是切线长,可得CD⊥EO,CD⊥AB,证得AB∥EO,可得E是AC 的中点.即可知点E运动到AC中点时时,直线ED与⊙O相切.
解答 解:(1)连接CD,
∵BC为⊙O的直径
∴∠CDB=90°,
在Rt△ACB 中,∠ACB=90°,AC=3cm,BC=4cm,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5(cm),
∵${S_{△ABC}}=\frac{1}{2}AC•BC=\frac{1}{2}CD•AB$,
∴CD=$\frac{AC•BC}{AB}$=$\frac{12}{5}$,
又在Rt△ADC中,AD2=AC2-CD2,
∴AD=$\sqrt{9-{{(\frac{12}{5})}^2}}=\frac{9}{5}$(cm);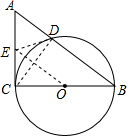
(2)如图,连接ED,EO,
∵ED与⊙O相切,
∴∠EDO=ECO=90°,
∴ED,EC是切线长,
∴CD⊥EO,
∵CD⊥AB,
∴AB∥EO,
∴CO:OB=CE:AE,
∵OC=OB,
∴AE=CE,
即E是AC 的中点.
∴E在AC的中点处,直线ED 与⊙O相切.
点评 此题考查了切线的性质与判定、切线长定理以及勾股定理.注意准确作出辅助线是解此题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是x=-3.
如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是x=-3.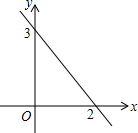 一次函数y=kx+b(k≠0)的图象如图所示,当x=0时,y的值是3.
一次函数y=kx+b(k≠0)的图象如图所示,当x=0时,y的值是3.