题目内容
 如图,在半径为2的⊙A中,点E为优弧
如图,在半径为2的⊙A中,点E为优弧 |
| BEC |
 |
| EC |
(1)求弦BC的长;
(2)求阴影部分的面积y关于x的函数解析式,并写出自变量x的取值范围;
(3)试分析比较阴影部分的面积y与扇形ABC的面积S的大小关系.
考点:圆的综合题
专题:
分析:(1)根据∠BAC的度数,我们可得出△BAC应是个等边三角形,那么BC的长就是半径的长.
(2)在(1)中已经求得了BC的长,又知道了D到BC的距离也就是BC上的高,那么可根据三角形的面积计算公式得出y,x的函数关系式.如果过A作AH⊥BC于H,那么x的最大值就是AH+半径的长,那么可在直角△AHB中求出AH的长也就求出了x的取值范围.
(3)先计算出扇形BAC的面积,然后根据y与S的大小关系的不同得出不同的自变量的取值范围即可.
(2)在(1)中已经求得了BC的长,又知道了D到BC的距离也就是BC上的高,那么可根据三角形的面积计算公式得出y,x的函数关系式.如果过A作AH⊥BC于H,那么x的最大值就是AH+半径的长,那么可在直角△AHB中求出AH的长也就求出了x的取值范围.
(3)先计算出扇形BAC的面积,然后根据y与S的大小关系的不同得出不同的自变量的取值范围即可.
解答: 解:(1)∵AB=AC,∠BAC=60°
解:(1)∵AB=AC,∠BAC=60°
∴△BAC是等边三角形
∴BC=AB=2;
(2)如图,过点A作AH⊥BC于H点,则BH=
BC=1.
y=S△DBC+S扇形ABC-S△ABC=
•2x+
-
×2×2×sin60°=x+
π-
,
即y=x+
π-
.
在Rt△ABH中,由勾股定理得到:AH2=AB2-BH2=3
∴AH=
,
∴0<x≤2+
;
(3)y-S=x-
.
当x=
时,y-S=0,则y=S;
当0<x<
时,y-S<0,则y<S;
当x>
时,y-S>0,则y>S.
 解:(1)∵AB=AC,∠BAC=60°
解:(1)∵AB=AC,∠BAC=60°∴△BAC是等边三角形
∴BC=AB=2;
(2)如图,过点A作AH⊥BC于H点,则BH=
| 1 |
| 2 |
y=S△DBC+S扇形ABC-S△ABC=
| 1 |
| 2 |
| 60π×22 |
| 360 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
即y=x+
| 2 |
| 3 |
| 3 |
在Rt△ABH中,由勾股定理得到:AH2=AB2-BH2=3
∴AH=
| 3 |
∴0<x≤2+
| 3 |
(3)y-S=x-
| 3 |
当x=
| 3 |
当0<x<
| 3 |
当x>
| 3 |
点评:本题主要考查了圆的综合题.解题时,利用了勾股定理、垂径定理、等边三角形的判定与性质以及扇形面积的计算.解(3)题时,一定要分类讨论,以防漏解.

练习册系列答案
相关题目
 有一个数值转换器,原理如图,则当输入的x为144时,输出的y是( )
有一个数值转换器,原理如图,则当输入的x为144时,输出的y是( )| A、12 | ||
B、2
| ||
C、2
| ||
D、3
|
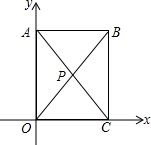 如图,长方形ABCO对角线BO与AC的交点P到相对两边距离相等.若C点(2,0),P(1,2),请写出A,B坐标,你发现A,P,C三点横坐标有什么关系呢?纵坐标呢?
如图,长方形ABCO对角线BO与AC的交点P到相对两边距离相等.若C点(2,0),P(1,2),请写出A,B坐标,你发现A,P,C三点横坐标有什么关系呢?纵坐标呢? 已知线段a,b(如图),画出线段AB,使AB=a+2b.
已知线段a,b(如图),画出线段AB,使AB=a+2b. 如图,AD平分∠EAC,AD∥BC,试探索∠B与∠C的数量关系,写出你的结论并说明理由.
如图,AD平分∠EAC,AD∥BC,试探索∠B与∠C的数量关系,写出你的结论并说明理由. 如图,AD、BE、CF相交于点O,∠AOC=110°,∠BOD=130°,求∠COE.
如图,AD、BE、CF相交于点O,∠AOC=110°,∠BOD=130°,求∠COE.