题目内容
19.抛物线y=x2-(2a+1)x+a-1与x轴的两个交点分别位于点(1,0)的两旁,则a的取值范围为a>-1.分析 设抛物线y=x2-(2a+1)x+a-1与x轴的两个交点的坐标分别为(α,0)、(β,0),且α<β,因为α、β是关于x的方程x2-(2a+1)x+a-1=0的两个不相等的实数根,所以由根与系数关系得:α+β=2a+1,αβ=a-1,再根据抛物线y=x2-(2a+1)x+a-1与x轴的两个交点分别位于点(1,0)的两旁可得α<1,β>1,进而可求出a的取值范围.
解答 解:∵抛物线y=x2-(2a+1)x+a-1与x轴的两个交点在(1,0)两旁,
∴关于x的方程x2-(2a+1)x+a-1=0有两个不相等的实数根,
∴△=b2-4ac>0,
即:(2a+1)2-4(a-1)>0,
整理得:4a2+5>0,
∴a为任意实数①.
设抛物线y=x2-(2a+1)x+a-1与x轴的两个交点的坐标分别为(α,0)、(β,0),且α<β,
则α、β是关于x的方程x2-(2a+1)x+a-1=0的两个不相等的实数根,
由根与系数关系得:α+β=2a+1,αβ=a-1,
∵抛物线y=x2-(2a+1)x+a-1与x轴的两个交点分别位于点(1,0)的两旁,
∴α<1,β>1,
∴(α-1)(β-1)<0,
∴αβ-(α+β)+1<0,
∴(a-1)-(2a+1)+1<0,
解得:a>-1②,
由①、②得m的取值范围是a>-1,
故答案为:a>-1.
点评 本题考查了抛物线与x轴的交点问题,注:当抛物线y=ax2+bx+c与轴有两个交点时,一元二次方程ax2+bx+c=0有两个不等的实数根即△>0;当抛物线y=ax2+bx+c与轴有一个交点时,一元二次方程ax2+bx+c=0有两个相等的实数根即△=0;当抛物线y=ax2+bx+c与轴无交点时,一元二次方程ax2+bx+c=0无实数根即△<0.

练习册系列答案
相关题目
7.有一组按规律排列的数:1,2,4,8,16,32,…,第2012个数应是( )
| A. | 22012 | B. | 22011 | C. | 22010 | D. | 22009 |
14.如图,△ABC与△A′B′C′关于直线MN对称,P为MN上任意一点,下列说法不正确的是( )
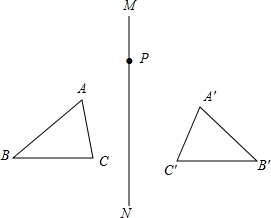

| A. | AP=A′P | B. | MN垂直平分AA′,CC′ | ||
| C. | 这两个三角形的面积相等 | D. | 直线AB、A′B的交点不一定在MN上 |
11.已知线段AC=1厘米,BC=3厘米,则线段AB的长度为( )
| A. | 4厘米 | B. | 2厘米 | C. | 2厘米或4厘米 | D. | 不能确定 |
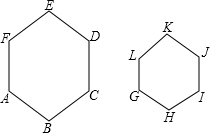 如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论中:
如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论中: