题目内容
设实数a,b满足a2=2-2a,b2=2-2b,则 = .
= .
【答案】分析:因为a2=2-2a,b2=2-2b可以变化为 即
即 ,从而可以求出a,b,然后把它们的值代入得原式即可求出结果.
,从而可以求出a,b,然后把它们的值代入得原式即可求出结果.
解答:解:∵a2=2-2a,b2=2-2b,
∴可以变化为 ,
,
即 ,
,
解得a=± -1,b=
-1,b= ,
,
把 代入得原式=
代入得原式= +1;
+1;
把 代入得原式=-5;
代入得原式=-5;
把 代入得原式=-5;
代入得原式=-5;
把 代入得原式=1-
代入得原式=1- .
.
所以此题的答案为 +1,1-
+1,1- ,-5.
,-5.
故填空答案: +1,1-
+1,1- ,-5.
,-5.
点评:本题的关键是利用完全平方公式先求得a,b的值,再分情况分别代入求值计算.
 即
即 ,从而可以求出a,b,然后把它们的值代入得原式即可求出结果.
,从而可以求出a,b,然后把它们的值代入得原式即可求出结果.解答:解:∵a2=2-2a,b2=2-2b,
∴可以变化为
 ,
,即
 ,
,解得a=±
 -1,b=
-1,b= ,
,把
 代入得原式=
代入得原式= +1;
+1;把
 代入得原式=-5;
代入得原式=-5;把
 代入得原式=-5;
代入得原式=-5;把
 代入得原式=1-
代入得原式=1- .
.所以此题的答案为
 +1,1-
+1,1- ,-5.
,-5.故填空答案:
 +1,1-
+1,1- ,-5.
,-5.点评:本题的关键是利用完全平方公式先求得a,b的值,再分情况分别代入求值计算.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
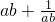 的值.
的值. =________.
=________.