题目内容
设实数a、b满足a2-8a+6=0及6b2-8b+1=0，求ab+| 1 | ab |
分析：方程6b2-8b+1=0可化为：则(
)2-8×
+6=0，把a，
看成方程x2-8x+6=0的两个根，根据根与系数的关系即可求解．
| 1 |
| b |
| 1 |
| b |
| 1 |
| b |
解答：解：由于6b2-8b+1=0，
则b≠0，
则(
)2-8×
+6=0，
当a≠
时，
则a，
为方程x2-8x+6=0的两个根，
不妨设x1=a，x2=
，
则x1+x2=8，x1x2=6，
所以ab+
=
+
=
=
=
，
当a=
时，即ab=1，因此ab+
=2．
综上：当a≠
时，ab+
=
；
当a=
时，ab+
=2．
则b≠0，
则(
| 1 |
| b |
| 1 |
| b |
当a≠
| 1 |
| b |
则a，
| 1 |
| b |
不妨设x1=a，x2=
| 1 |
| b |
则x1+x2=8，x1x2=6，
所以ab+
| 1 |
| ab |
| x1 |
| x2 |
| x2 |
| x1 |
| (x1+x2)2-2x1x2 |
| x1x2 |
| 64-12 |
| 6 |
| 26 |
| 3 |
当a=
| 1 |
| b |
| 1 |
| ab |
综上：当a≠
| 1 |
| b |
| 1 |
| ab |
| 26 |
| 3 |
当a=
| 1 |
| b |
| 1 |
| ab |
点评：本题考查了根与系数的关系及代数式求值，难度适中，关键是掌握x1，x2是方程x2+px+q=0的两根时，x1+x2=-p，x1x2=q．
练习册系列答案
习题精选系列答案
相关题目
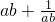的值．
=________．
= ．