题目内容
用配方法解方程：x2-61x+60=0．
考点：解一元二次方程-配方法
专题：
分析：首先移项，然后方程左右两边加上一次项系数的一半的平方，则左边是完全平方式，右边是常数，即可利用直接开平方法求解．
解答：解：移项，得：x2-61x=-60，
配方x2-61x+
=-60+
，
则（x-
）2=
，
则x-
=±
，
则x1=60，x2=1．
配方x2-61x+
| 3721 |
| 4 |
| 3721 |
| 4 |
则（x-
| 61 |
| 2 |
| 1321 |
| 4 |
则x-
| 61 |
| 2 |
| 59 |
| 2 |
则x1=60，x2=1．
点评：本题考查了配方法解方程，配方法的一般步骤：
（1）把常数项移到等号的右边；
（2）把二次项的系数化为1；
（3）等式两边同时加上一次项系数一半的平方．
选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．
（1）把常数项移到等号的右边；
（2）把二次项的系数化为1；
（3）等式两边同时加上一次项系数一半的平方．
选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．
练习册系列答案
53随堂测系列答案
相关题目
把分式
中的字母x、y的值都扩大10倍，则分式的值（ ）
| 5x |
| xy |
| A、扩大5倍 | ||
| B、扩大10倍 | ||
| C、不变 | ||
D、是原来的
|
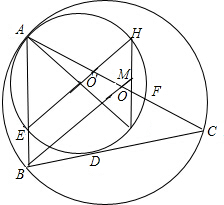已知⊙O与⊙O′内切于点A，⊙O的弦BC与⊙O′切于点D，AB、AC与⊙O′分别交于点E、F，AG、EH为⊙O′直径，BO延长线交GH于点M．