题目内容
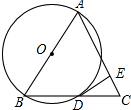 如图,在△ABC中,以AB为直径作⊙O交BC于D,DE交AC于点E.
如图,在△ABC中,以AB为直径作⊙O交BC于D,DE交AC于点E.(1)若AB=AC,且DE⊥AC.求证:DE是⊙O的切线.
(2)若AB=AC,DE切⊙O于点D.求证:DE⊥AC.
(3)若DE切⊙O于点D,且DE⊥AC.求证:AB=AC.
考点:切线的判定与性质
专题:
分析:(1)连结OD,就有OD=OB,得出∠B=∠ODB,根据AB=AC就可以得出∠B=∠C,就可以得出∠ODB=∠C,得出OD∥AC,得出∠ODE=∠CED,由DE⊥AC就可以得出∠DEC=90°而得出结论.
(2)连结OD,DE切⊙O于点D就有OD⊥DE,得出∠ODE=90°,就有OD=OB,得出∠B=∠ODB,根据AB=AC就可以得出∠B=∠C,就可以得出∠ODB=∠C,得出OD∥AC,得出∠ODE=∠CED,得出∠DEC=90°而得出结论.
(3)连结OD,DE切⊙O于点D就有OD⊥DE,得出∠ODE=90°,由DE⊥AC就可以得出∠DEC=90°,得出∠ODE=∠CED,就有OD∥AC,∠ODB=∠C,OD=OB,得出∠B=∠ODB,就有∠B=∠C,进而得出AB=AC.
(2)连结OD,DE切⊙O于点D就有OD⊥DE,得出∠ODE=90°,就有OD=OB,得出∠B=∠ODB,根据AB=AC就可以得出∠B=∠C,就可以得出∠ODB=∠C,得出OD∥AC,得出∠ODE=∠CED,得出∠DEC=90°而得出结论.
(3)连结OD,DE切⊙O于点D就有OD⊥DE,得出∠ODE=90°,由DE⊥AC就可以得出∠DEC=90°,得出∠ODE=∠CED,就有OD∥AC,∠ODB=∠C,OD=OB,得出∠B=∠ODB,就有∠B=∠C,进而得出AB=AC.
解答: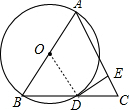 证明:(1)连结OD,
证明:(1)连结OD,
∴OD=OB,
∴∠B=∠ODB.
∵AB=AC,
∴∠B=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∴∠ODE=∠CED.
∵DE⊥AC,
∴∠DEC=90°,
∴∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)连结OD,
∴OD=OB,
∴∠B=∠ODB.
∵DE切⊙O于点D,
∴OD⊥DE,
∴∠ODE=90°.
∵AB=AC,
∴∠B=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∴∠ODE=∠CED,
∴∠DEC=90°
∴DE⊥AC;
(3)连结OD,
∴OD=OB,
∴∠B=∠ODB.
∵DE切⊙O于点D,
∴OD⊥DE,
∴∠ODE=90°.
∵DE⊥AC,
∴∠DEC=90°,
∴∠ODE=∠CED,
∴OD∥AC,
∴∠ODB=∠C,
∴∠B=∠C,
∴AB=AC.
 证明:(1)连结OD,
证明:(1)连结OD,∴OD=OB,
∴∠B=∠ODB.
∵AB=AC,
∴∠B=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∴∠ODE=∠CED.
∵DE⊥AC,
∴∠DEC=90°,
∴∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)连结OD,
∴OD=OB,
∴∠B=∠ODB.
∵DE切⊙O于点D,
∴OD⊥DE,
∴∠ODE=90°.
∵AB=AC,
∴∠B=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∴∠ODE=∠CED,
∴∠DEC=90°
∴DE⊥AC;
(3)连结OD,
∴OD=OB,
∴∠B=∠ODB.
∵DE切⊙O于点D,
∴OD⊥DE,
∴∠ODE=90°.
∵DE⊥AC,
∴∠DEC=90°,
∴∠ODE=∠CED,
∴OD∥AC,
∴∠ODB=∠C,
∴∠B=∠C,
∴AB=AC.
点评:本题考查了切线的判定及性质的运用,等腰三角形的判定及性质的运用,垂直的判定及性质的运用,解答时运用等腰三角形的性质及切线的性质求解是关键.

练习册系列答案
相关题目
在下列长度的各组线段中,能构成直角三角形的是( )
| A、3,5,9 | ||||||
B、1,
| ||||||
| C、4,6,8 | ||||||
D、
|
在数:3.14159,1.010010001…,7.56,π,
中,无理数的个数有( )
| 22 |
| 7 |
| A、1个 | B、2个 | C、3个 | D、4个 |
定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“凤凰”方程.已知方程a1x2+b1x+c1=0(a≠0)是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
| A、a1=b1 |
| B、a1=c1 |
| C、b1=c1 |
| D、a1=b1=c1 |
 如图,Rt△ABC中∠C=90°,D在BC上,AB⊥BE,EF⊥BC于F,∠EAB=∠DAC.求证:
如图,Rt△ABC中∠C=90°,D在BC上,AB⊥BE,EF⊥BC于F,∠EAB=∠DAC.求证: