题目内容
8.化简:$\frac{{x}^{2}-x-2+(x-1)\sqrt{{x}^{2}-4}}{{x}^{2}+x-2+(x+1)\sqrt{{x}^{2}-4}}$.(x>2)分析 原式变形后,约分即可得到结果.
解答 解:原式=$\frac{(x-2)(x+1)+(x-1)\sqrt{x-2}•\sqrt{x+2}}{(x+2)(x-1)+(x+1)\sqrt{x-2}•\sqrt{x+2}}$
=$\frac{\sqrt{x-2}[\sqrt{x-2}(x+1)+(x-1)\sqrt{x+2}]}{\sqrt{x+2}[\sqrt{x+2}(x-1)+(x+1)\sqrt{x-2}]}$
=$\frac{\sqrt{x-2}}{\sqrt{x+2}}$=$\frac{\sqrt{{x}^{2}-4}}{x+2}$.
点评 此题考查了二次根式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
18.两直线平行,一对同旁内角的平分线互相( )
| A. | 平行 | B. | 垂直 | C. | 相等 | D. | 无法确定 |
13.在平面直角坐标系中有一点P(-3,4),则点P到原点O的距离是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
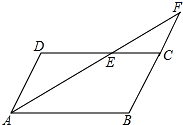 如图,平行四边形ABCD中,AB=5,AD=2,AE平分∠DAB交DC于E点,交BC的延长线于F点,则CF=3.
如图,平行四边形ABCD中,AB=5,AD=2,AE平分∠DAB交DC于E点,交BC的延长线于F点,则CF=3.
 如图,在一块半径为R的圆形板材上,冲去半径为r的四个小圆,小刚测得R=6.8cm,r=1.6
如图,在一块半径为R的圆形板材上,冲去半径为r的四个小圆,小刚测得R=6.8cm,r=1.6