题目内容
如图已知AD是△ABC中∠BAC的平分线，∠ACE是△ABC的外角，若∠DAC=35°，∠ACE=106°，求∠B的数．
解：∵AD是△ABC中∠BAC的平分线，且∠DAC=35°，
∴∠BAC=2∠DAC=70°，
又∠ACE是△ABC的外角，且∠ACE=106°，
∴∠ACE=∠B+∠BAC，即106°=∠B+70°，
则∠B=36°．
分析：由AD为角平分线，得到∠BAC=2∠DAC，由∠DAC的度数求出∠BAC的度数，又∠ACE为三角形ABC的外角，利用三角形的外角等于与它不相邻的两个内角之和列出等式，将∠BAC与∠ACE的度数代入，即可求出∠B的度数．
点评：此题考查了角平分线的定义，以及三角形的外角性质，熟练掌握外角性质是解本题的关键．
∴∠BAC=2∠DAC=70°，
又∠ACE是△ABC的外角，且∠ACE=106°，
∴∠ACE=∠B+∠BAC，即106°=∠B+70°，
则∠B=36°．
分析：由AD为角平分线，得到∠BAC=2∠DAC，由∠DAC的度数求出∠BAC的度数，又∠ACE为三角形ABC的外角，利用三角形的外角等于与它不相邻的两个内角之和列出等式，将∠BAC与∠ACE的度数代入，即可求出∠B的度数．
点评：此题考查了角平分线的定义，以及三角形的外角性质，熟练掌握外角性质是解本题的关键．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
17、如图所示，已知AD是△ABC的角平分线，DE∥AC交AB于点E，DF∥AB交AC于点F，
如图已知：D、E是△ABC的边AB、AC上的点，且∠ADE=∠C，求证：AD•AB=AE•AC．
如图，已知AD是等腰△ABC的底边BC上的高，BC=2，AB=3，则AD=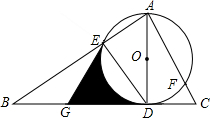
（2013•本溪二模）如图，已知AD是△ABC中BC边上的高，以AD为直径的⊙O分别交AB、AC于点E、F，点G是BD的中点