题目内容
17. 如图所示,若△ABC和△ADE都是等边三角形,线段BD=10cm,试求线段CE的长,并说明理由.
如图所示,若△ABC和△ADE都是等边三角形,线段BD=10cm,试求线段CE的长,并说明理由.
分析 根据等边三角形的性质求出AE=AD,AB=AC,∠EAC=∠DAB,再根据SAS证出△EAC≌△DAB,得出BD=CE,从而求出CE的长.
解答 解:∵△ABC和△ADE都是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠CAB=60°,
∴∠EAD+∠CAD=∠CAB+∠CAD,
∴∠EAC=∠DAB,
在△EAC和△DAB中,
$\left\{\begin{array}{l}{EA=AD}\\{∠EAC=DAB}\\{AC=AB}\end{array}\right.$,
∴△EAC≌△DAB (SAS),
∴BD=CE,
∵BD=10cm,
∴CE=10cm.
点评 此题考查了全等三角形的判定与性质,用到的知识点是全等三角形的判定与性质、等边三角形的性质,关键是根据∠EAD+∠CAD=∠CAB+∠CAD,求出∠EAC=∠DAB.

练习册系列答案
相关题目
7.在$\frac{a}{π}$,$\frac{1}{x+1}$,$\frac{1}{5}$x+y,$\frac{{a}^{2}}{a}$,-2x5中.其中是分式的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.抛物线y=x2+2x-2的图象最高点的坐标是( )
| A. | (2,-2) | B. | (1,-2) | C. | (1,-3) | D. | (-1,-3) |
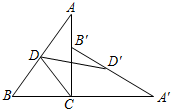 如图,将Rt△ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置,D,D′分别是AB,A′B′的中点,且CD=$\frac{1}{2}AB$,已知AC=8cm,BC=6cm,求线段DD′的长.
如图,将Rt△ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置,D,D′分别是AB,A′B′的中点,且CD=$\frac{1}{2}AB$,已知AC=8cm,BC=6cm,求线段DD′的长. 已知:如图所示,要在高AD=80mm,底边BC=120mm的三角形余料中截出一个正方形板材PQMN,AD与PN交于E.求正方形的边长.
已知:如图所示,要在高AD=80mm,底边BC=120mm的三角形余料中截出一个正方形板材PQMN,AD与PN交于E.求正方形的边长.