题目内容
如图，在边长为1的小正方形网格中，⊙O的圆心在格点上，AB为直径，BC交⊙O于点D，则cos∠AED=考点：圆周角定理,勾股定理,锐角三角函数的定义
专题：网格型
分析：先在Rt△ABC中利用勾股定理计算出BC=
，再利用余弦的定义得到cos∠ABC=
=
，然后根据圆周角定理得∠AED=∠ABD，所以cos∠AED=
．
| 5 |
| AB |
| BC |
2
| ||
| 5 |
2
| ||
| 5 |
解答：解：在Rt△ABC中，∵AB=2，AC=1，
∴BC=
=
，
∴cos∠ABC=
=
=
，
∵∠AED=∠ABD，
∴cos∠AED=
．
故答案为
．
∴BC=
| AC2+AB2 |
| 5 |
∴cos∠ABC=
| AB |
| BC |
| 2 | ||
|
2
| ||
| 5 |
∵∠AED=∠ABD，
∴cos∠AED=
2
| ||
| 5 |
故答案为
2
| ||
| 5 |
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．充分利用网格的特点构建直角三角形．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
某人要建一个长方形的养鸡场，它的一边靠墙（墙长15m）另三边用木栅栏围成，中间又用木栅栏分割成三个部分，木栅栏的总长为36m，鸡场的总面积为72m2．求整个鸡场的长和宽．月球的质量约为73400 000 000亿吨，用科学记数法表示这个数是（ ）
| A、734×108亿吨 |
| B、73.4×109亿吨 |
| C、7.34×1010亿吨 |
| D、0.734×1011亿吨 |
如图，∠1的同位角是
如图所示，在O点的观测站测得渔船A、B的方向分别为北偏东45°，南偏西30°，为了减少相互干扰并取得较好的捕鱼效益，渔船C恰好位于∠AOB的平分线上，求渔船C相对观测站的方向．下列关于邻补角的说法，正确的是（ ）
| A、和为180°的两个角互为邻补角 |
| B、有公共顶点且互补的两个角互为邻补角 |
| C、有一条公共边且有一条公共边，另一边互为反向延长线的两个角互为邻补角 |
| D、有公共顶点且有一条公共边，另一边互为反向延长线的两个角互为邻补角 |
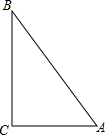如图，点A表示小雨家，点B表示小樱家，点C表示小丽家，她们三家恰好组成一个直角三角形，其中AC⊥BC，AC=900米，BC=1200米，AB=1500米．