题目内容
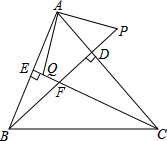 BD、CE分别是△ABC的边AC、AB上的高,P在BD的延长线上,且BP=AC,点Q在CE上,CQ=AB.求证:
BD、CE分别是△ABC的边AC、AB上的高,P在BD的延长线上,且BP=AC,点Q在CE上,CQ=AB.求证:(1)AP=AQ;
(2)AP⊥AQ.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)由于BD⊥AC,CE⊥AB,可得∠ABD=∠ACE,又有对应边的关系,进而得出△ABP≌△QCA,即可得出结论.
(2)在(1)的基础上,证明∠PAQ=90°即可.
(2)在(1)的基础上,证明∠PAQ=90°即可.
解答:证明:(1)∵BD⊥AC,CE⊥AB(已知),
∴∠BEC=∠BDC=90°,
∴∠ABD+∠BAC=90°,∠ACE+∠BAC=90°(垂直定义),
∴∠ABD=∠ACE(等角的余角相等),
在△ABP和△QCA中,
,
∴△ABP≌△QCA(SAS),
∴AP=AQ(全等三角形对应边相等).
(2)由(1)可得∠CAQ=∠P(全等三角形对应角相等),
∵BD⊥AC(已知),即∠P+∠CAP=90°(直角三角形两锐角互余),
∴∠CAQ+∠CAP=90°(等量代换),即∠QAP=90°,
∴AP⊥AQ(垂直定义).
∴∠BEC=∠BDC=90°,
∴∠ABD+∠BAC=90°,∠ACE+∠BAC=90°(垂直定义),
∴∠ABD=∠ACE(等角的余角相等),
在△ABP和△QCA中,
|
∴△ABP≌△QCA(SAS),
∴AP=AQ(全等三角形对应边相等).
(2)由(1)可得∠CAQ=∠P(全等三角形对应角相等),
∵BD⊥AC(已知),即∠P+∠CAP=90°(直角三角形两锐角互余),
∴∠CAQ+∠CAP=90°(等量代换),即∠QAP=90°,
∴AP⊥AQ(垂直定义).
点评:本题主要考查了全等三角形的判定及性质问题,能够熟练掌握并运用.

练习册系列答案
相关题目
 如图,直线a表示一条公路,点A、B表示两个乡镇,如果要在公路旁(直线a上)修一个车站S,使得AS=BS,请作出点S.
如图,直线a表示一条公路,点A、B表示两个乡镇,如果要在公路旁(直线a上)修一个车站S,使得AS=BS,请作出点S.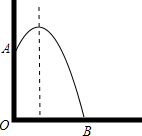 如图,某栋建筑物从10米高的窗口A用水管向外喷水,喷出的水流呈抛物线状,如抛物线的函数关系式是y=-
如图,某栋建筑物从10米高的窗口A用水管向外喷水,喷出的水流呈抛物线状,如抛物线的函数关系式是y=-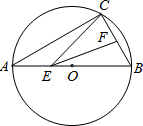 如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E从A点出发沿着A→B方向运动,连接EF、CE,则EF+CE最小值是
如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E从A点出发沿着A→B方向运动,连接EF、CE,则EF+CE最小值是