题目内容
13. 如图:∠1=30°,OC⊥OB,且OC平分∠AOD.求
如图:∠1=30°,OC⊥OB,且OC平分∠AOD.求(1)∠DOC的度数;
(2)∠BOD的度数.
分析 (1)根据垂直定义可得∠BOC=90°,再根据角的和差关系可得∠AOC的度数,再利用角平分线的定义可得∠COD的度数.
(2)利用∠DOC,∠COA,∠1的度数可得∠DOB的度数.
解答 解:(1)∵OC⊥OB,
∴∠BOC=90°,
∵∠1=30°,
∴∠COA=60°,
∵OC平分∠AOD,
∴∠DOC=∠AOC=60°;
(2)∵∠DOC=∠AOC=60°,∠1=30°,
∴∠BOD=60°+60°+30°=150°.
点评 此题主要考查了垂线,以及角的计算,关键是理清角之间的关系.

练习册系列答案
相关题目
8. 如图:AB=AC,∠B=∠C,且AB=5,AE=2,则EC的长为( )
如图:AB=AC,∠B=∠C,且AB=5,AE=2,则EC的长为( )
 如图:AB=AC,∠B=∠C,且AB=5,AE=2,则EC的长为( )
如图:AB=AC,∠B=∠C,且AB=5,AE=2,则EC的长为( )| A. | 2 | B. | 3 | C. | 5 | D. | 2.5 |
18. 如图,将长方形纸片ABCD的角C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若FH平分∠BFE,则∠GFH的度数( )
如图,将长方形纸片ABCD的角C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若FH平分∠BFE,则∠GFH的度数( )
 如图,将长方形纸片ABCD的角C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若FH平分∠BFE,则∠GFH的度数( )
如图,将长方形纸片ABCD的角C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若FH平分∠BFE,则∠GFH的度数( )| A. | 大于90° | B. | 小于90° | ||
| C. | 等于90° | D. | 随折痕GF位置的变化而变化 |
2.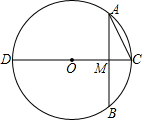 如图,已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长度为( )
如图,已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长度为( )
 如图,已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长度为( )
如图,已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长度为( )| A. | 4$\sqrt{5}$cm | B. | 3$\sqrt{5}$cm | C. | 2$\sqrt{5}$cm | D. | $\sqrt{5}$cm |
 在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(-1,a),B(3,a),且最低点的纵坐标为-4.
在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(-1,a),B(3,a),且最低点的纵坐标为-4. 如图,反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b图象的交点为A(m,1),B(-2,n),OA与x轴正方向的夹角为α,且tanα=$\frac{1}{4}$.
如图,反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b图象的交点为A(m,1),B(-2,n),OA与x轴正方向的夹角为α,且tanα=$\frac{1}{4}$. 如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠AOB等于100°.
如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠AOB等于100°. 尺规作图(要求保留作图痕迹):已知:线段a,b.求作:线段c,使得c=2b-a.
尺规作图(要求保留作图痕迹):已知:线段a,b.求作:线段c,使得c=2b-a.