题目内容
一个正方体的体积变为原来的n倍,则它的棱长变为原来的
- A.n倍
- B.
 倍
倍 - C.
 倍
倍 - D.
 倍
倍
D
分析:设原先体积为V,棱长为a,现在体积为nV,棱长为b,根据立方根的定义求出a和b,然后作比较.
解答:设原先体积为V,棱长为a,
则a=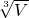 ,
,
现在体积为nV,棱长为b,
则b= ,
,
故 =
= =
= ,
,
故选D.
点评:本题主要考查立方根的知识点,解答此题的关键找出体积的变化,分别求出棱长,最后进行比较,得到答案.
分析:设原先体积为V,棱长为a,现在体积为nV,棱长为b,根据立方根的定义求出a和b,然后作比较.
解答:设原先体积为V,棱长为a,
则a=
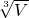 ,
,现在体积为nV,棱长为b,
则b=
 ,
,故
 =
= =
= ,
,故选D.
点评:本题主要考查立方根的知识点,解答此题的关键找出体积的变化,分别求出棱长,最后进行比较,得到答案.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
一个正方体的体积变为原来的n倍,则它的棱长变为原来的( )
| A、n倍 | |||
B、
| |||
C、
| |||
D、
|