题目内容
直线y=x+3与x轴交于A.与y轴交于B,以AB为一边作等边△ABC,则点C的坐标是 .
考点:一次函数图象上点的坐标特征,等边三角形的性质
专题:
分析:由直线y=3x+3与x轴交于点A,与y轴交于点B,分别令x=0,y=0,求出点A、B的坐标,再根据勾股定理求出AB,根据等边三角形的三边相等列出关于x、y的方程组,解方程组即可求得.
解答:解:令y=0,则x=-3,所以点A的坐标为(-3,0);
令x=0,则y=3,所以点B的坐标为(0,3).
∴OA=3,OB=3
在Rt△BAO中,根据勾股定理得:AB2=18,
∵等边△ABC中,AB=AB=BC,
设C(x,y),
∴
,解得
或
,
∴C(
,
)或(
,
).
故答案为(
,
)或(
,
).
令x=0,则y=3,所以点B的坐标为(0,3).
∴OA=3,OB=3
在Rt△BAO中,根据勾股定理得:AB2=18,
∵等边△ABC中,AB=AB=BC,
设C(x,y),
∴
|
|
|
∴C(
-3+3
| ||
| 2 |
3-3
| ||
| 2 |
-3-3
| ||
| 2 |
3+3
| ||
| 2 |
故答案为(
-3+3
| ||
| 2 |
3-3
| ||
| 2 |
-3-3
| ||
| 2 |
3+3
| ||
| 2 |
点评:此题考查了一次函数图象上点的坐标特征,和等边三角形的性质,关键是根据函数式求坐标,由勾股定理求出边长.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 如图,直线MN和∠AOB的两边分别相交于点C,D.已知∠1+∠2=180°,则图中与∠1相等的角(不含∠1)有( )
如图,直线MN和∠AOB的两边分别相交于点C,D.已知∠1+∠2=180°,则图中与∠1相等的角(不含∠1)有( )| A、1个 | B、2个 | C、3个 | D、4个 |
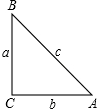 在Rt△ABC中,∠C=90°,BC,AC,AB三边的长分别为a,b,c,则sinA=
在Rt△ABC中,∠C=90°,BC,AC,AB三边的长分别为a,b,c,则sinA= 甲、已两工程队承包了修建长1620米的A、B两地间的公路,甲工程队从A地开始施工,3天后,乙工程队才从B地开始施工,甲乙两工程队共同施工6天后,乙工程队因另有任务提前离开,余下的任务由甲工程队单独再用6天完成,图中y甲、y乙分别表示甲、乙两工程队修建的公路长度y(米)与施工时间x(天)之间的函数关系.请你根据图象所提供的信息解答下列问题:
甲、已两工程队承包了修建长1620米的A、B两地间的公路,甲工程队从A地开始施工,3天后,乙工程队才从B地开始施工,甲乙两工程队共同施工6天后,乙工程队因另有任务提前离开,余下的任务由甲工程队单独再用6天完成,图中y甲、y乙分别表示甲、乙两工程队修建的公路长度y(米)与施工时间x(天)之间的函数关系.请你根据图象所提供的信息解答下列问题: