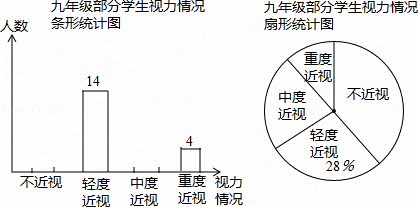
题目内容
如图,以OA1=2为底边做等腰三角形,使得第三个顶点C1恰好在直线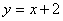 上,并以此向左、右依次类推,作一系列底边为2,第三个顶点在直线
上,并以此向左、右依次类推,作一系列底边为2,第三个顶点在直线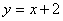 上的等腰三角形.
上的等腰三角形.
(1)底边为2,顶点在直线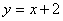 上且面积为21的等腰三角形位于图中什么位置?
上且面积为21的等腰三角形位于图中什么位置?
(2)求证:y轴右侧的每一个等腰三角形的面积都等于前后两个以腰为一边的三角形面积之和的
一半( 如:S右1=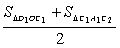 ,S右2
,S右2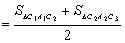 ).
).
(3)过D1、A1、C2三点画抛物线.问在抛物线上是否存在点P,使得△PD1C2的面积是△C1OD1与△C1A1C2面积和的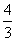 .若存在,请求出点P的坐标;若不存在,请说明理由.
.若存在,请求出点P的坐标;若不存在,请说明理由.

(1) ,
, ,
, 或
或 -----------2分
-----------2分
 ,或
,或 ,解得
,解得 或
或
∴在y轴的右边从左到右第10个或y轴的左边从右到左第12个.-----2分
(2)y轴右侧第n个等腰三角形An-1AnCn的底边两端点坐标为An-1 ,An
,An ,
,
∴面积为 ,--------------------2分
,--------------------2分
前后两个非等腰三角形的面积和为 .------2分
.------2分
∴y轴右侧的每一个等腰三角形的面积都等于前后两个以腰为一边的三角形面积之和的一半.
(3)过D1, A1, C2三点的抛物线解析式为: ,---------1分
,---------1分
△C1OD1与△C1A1C2面积和等于2
 ×2×3=6,-------------------------1分
×2×3=6,-------------------------1分
当点P在直线下方时:
解得:
 ,
, ;∴
;∴ ,
,
∴ ---------------------------------1分
---------------------------------1分
当点P在直线上方时:
得: ,即
,即 ,
, ,
, ,
,
∴ ----------------------------1分
----------------------------1分
(注:第(3)题另解:用点到直线距离公式,可4个点同时求得,解法如下:
设点P(x,  ),则P到
),则P到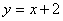 的距离d
的距离d

∴S△PD1C2= D1C2·d=
D1C2·d=

 =8,解得4个点P坐标.)
=8,解得4个点P坐标.)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案如图,将三角形的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )

|
| A. | 10° | B. | 15° | C. | 20° | D. | 25° |

 时,kx+b<0。
时,kx+b<0。
 重合,则点
重合,则点
 的正方形ABCD.求作该正方形绕点A逆时针旋转30°后的正方形
的正方形ABCD.求作该正方形绕点A逆时针旋转30°后的正方形 .(说明:请用无刻度的直尺和圆规作图,并保留作图痕迹)
.(说明:请用无刻度的直尺和圆规作图,并保留作图痕迹)

 ,则( )
,则( )