题目内容
一队学生去军事训练,走到半路,队长有事要从队头通知到队尾,通讯员以18/分的速度从队头至队尾又返回,已知队伍的行进速度为14米/分.问:若已知队伍长320米,则通讯员几钟返回?若已知通讯员用了25分钟,则队伍长为多少米?
考点:一元一次方程的应用
专题:
分析:通讯员以18米/分的速度从队头至队尾,属于相遇问题,通讯员与队尾行驶的路程之和等于队伍的长度320米,二者行驶的速度之和是18+14=32米/分,由此即可求出行至队尾时用的时间是320÷(18+14)=10分钟;返回时,属于追及问题,通讯员行驶的路程比队头行驶的路程多队伍的长度320米,二者的速度之差是18-14=4米/秒,由此可得所用的时间是:320÷(18-14)=80分钟,再利用加法原理即可解答;
设队伍的长度是x米,则根据行至队尾的时间+返回队头的时间之和=25分钟,列出方程即可解答.
设队伍的长度是x米,则根据行至队尾的时间+返回队头的时间之和=25分钟,列出方程即可解答.
解答:解:320÷(18+14)+320÷(18-14)
=320÷32+320÷4
=10+80
=90(分钟);
设队伍长是x米,根据题意可得方程:
+
=25,
解得:x=
,
答:若已知队伍长320米,则通讯员90分钟返回;若已知通讯员用了25分钟,则队伍长为
米.
=320÷32+320÷4
=10+80
=90(分钟);
设队伍长是x米,根据题意可得方程:
| x |
| 18+14 |
| x |
| 18-14 |
解得:x=
| 800 |
| 9 |
答:若已知队伍长320米,则通讯员90分钟返回;若已知通讯员用了25分钟,则队伍长为
| 800 |
| 9 |
点评:此题主要考查了一元一次方程的应用,解决本题的关键是得到通讯员所用时间的等量关系,难点是得到当为追及问题时,速度为两者的速度之差,路程为队伍长度;当为相遇问题时,速度为两者的速度之和,路程为队伍长度.

练习册系列答案
相关题目
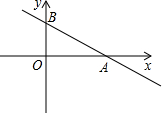 在平面直角坐标系中,点O为坐标原点,直线y=-
在平面直角坐标系中,点O为坐标原点,直线y=- 如图,已知
如图,已知