题目内容
 如图,已知
如图,已知 |
| AB |
 |
| AB |
考点:圆心角、弧、弦的关系,含30度角的直角三角形,等腰直角三角形
专题:计算题
分析:作DG⊥OB于G,EH⊥OB于H,如图,由C是
的中点,根据垂径定理的推论得OD⊥AB,而△AOB为等腰直角三角形,则∠OBA=45°,所以△ODB为等腰直角三角形,得到DG=
OB,再证明四边形DEHG为矩形,得到EH=DG=
OB,则EH=
OE,根据含30度的直角三角形三边的关系即可得到∠EOB=30°.
 |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:作DG⊥OB于G,EH⊥OB于H,如图,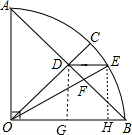
∵C是
的中点,
∴OD⊥AB,
∵OA⊥OB,
而OA=OB,
∴△AOB为等腰直角三角形,
∴∠OBA=45°,
∴△ODB为等腰直角三角形,
∴DG=
OB,
∵DE∥GH,DG⊥OB,EH⊥OB,
∴四边形DEHG为矩形,
∴EH=DG=
OB,
而OB=OE,
∴EH=
OE,
∴∠EOH=30°,
即∠EOB=30°.

∵C是
 |
| AB |
∴OD⊥AB,
∵OA⊥OB,
而OA=OB,
∴△AOB为等腰直角三角形,
∴∠OBA=45°,
∴△ODB为等腰直角三角形,
∴DG=
| 1 |
| 2 |
∵DE∥GH,DG⊥OB,EH⊥OB,
∴四边形DEHG为矩形,
∴EH=DG=
| 1 |
| 2 |
而OB=OE,
∴EH=
| 1 |
| 2 |
∴∠EOH=30°,
即∠EOB=30°.
点评:本题考查了圆心角、弧、弦的关系:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了等腰直角三角形的判定与性质.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
3.14159…取精确到百分位的近似值是( )
| A、3.1 | B、3.14 |
| C、3.142 | D、3.1416 |
 如图,要测量水池对岸A、B的距离,如果测得AC、BC、DC的长分别为48m、72m、12m,那么只要在BC取点E,使CE=
如图,要测量水池对岸A、B的距离,如果测得AC、BC、DC的长分别为48m、72m、12m,那么只要在BC取点E,使CE=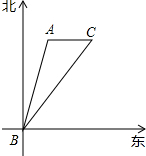 小明在课外实践活动中,在B处观测某建筑物A在北偏东15°方向,小明沿东北方向的公路BC以10km/h的速度前进,30min到达C处,测得A在正西方向,求建筑物A到BC的距离.
小明在课外实践活动中,在B处观测某建筑物A在北偏东15°方向,小明沿东北方向的公路BC以10km/h的速度前进,30min到达C处,测得A在正西方向,求建筑物A到BC的距离.