题目内容
 如图,直线AB交双曲线y=
如图,直线AB交双曲线y=| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:设A点坐标为(a,
),C点坐标为(b,0),根据线段中点坐标公式得到B点坐标为(
,
),利用反比例函数图象上点的坐标特征得到
•
=k,得到b=3a,
然后根据三角形面积公式得到
b•
=6,于是可计算出a=4.
| k |
| a |
| a+b |
| 2 |
| k |
| 2a |
| a+b |
| 2 |
| k |
| 2a |
然后根据三角形面积公式得到
| 1 |
| 2 |
| k |
| a |
解答:解:设A点坐标为(a,
),C点坐标为(b,0),
∵B恰为线段AC的中点,
∴B点坐标为(
,
),
∵B点在反比例函数图象上,
∴
•
=k,
∴b=3a,
∵S△OAC=6,
∴
b•
=6,
∴
•3a•
=6,
∴k=4.
故答案为4.
| k |
| a |
∵B恰为线段AC的中点,
∴B点坐标为(
| a+b |
| 2 |
| k |
| 2a |
∵B点在反比例函数图象上,
∴
| a+b |
| 2 |
| k |
| 2a |
∴b=3a,
∵S△OAC=6,
∴
| 1 |
| 2 |
| k |
| a |
∴
| 1 |
| 2 |
| k |
| a |
∴k=4.
故答案为4.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标满足两函数解析式.

练习册系列答案
相关题目
已知
=
-
,其中A、B为常数,则4A-B的值为( )
| 3x+4 |
| x2-x-2 |
| A |
| x-2 |
| B |
| x+1 |
| A、7 | B、9 | C、13 | D、5 |
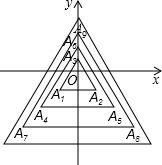 如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则顶点A2013的坐标是
如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则顶点A2013的坐标是