题目内容
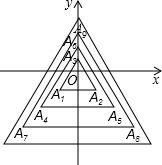 如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则顶点A2013的坐标是
如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则顶点A2013的坐标是考点:规律型:点的坐标
专题:
分析:先根据每一个三角形有三个顶点确定出A2013所在的三角形,再求出相应的三角形的边长以及A2013的纵坐标的长度,即可得解;
先根据每一个三角形有三个顶点确定出A2014所在的三角形,再求出相应的三角形的边长以及A2014的纵坐标的长度,即可得解.
先根据每一个三角形有三个顶点确定出A2014所在的三角形,再求出相应的三角形的边长以及A2014的纵坐标的长度,即可得解.
解答:解:∵2013÷3=671,
∴A2013是第671个等边三角形的第3个顶点,
第671个等边三角形边长为2×671=1342,
∴点A2013的纵坐标为1342×
-671=671
-671,
∴点A2013的坐标为(0,671
-671).
∵2014÷3=671…1,
∴A2014是第672个等边三角形的第1个顶点,
第672个等边三角形边长为2×672=1344,
∴点A2014的横坐标为
×(-1344)=-672,
∵边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,
∴点A2014的纵坐标为-672,
∴点A2014的坐标为(-672,-672).
故答案为:(0,671
-671);(-672,-672).
∴A2013是第671个等边三角形的第3个顶点,
第671个等边三角形边长为2×671=1342,
∴点A2013的纵坐标为1342×
| ||
| 2 |
| 3 |
∴点A2013的坐标为(0,671
| 3 |
∵2014÷3=671…1,
∴A2014是第672个等边三角形的第1个顶点,
第672个等边三角形边长为2×672=1344,
∴点A2014的横坐标为
| 1 |
| 2 |
∵边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,
∴点A2014的纵坐标为-672,
∴点A2014的坐标为(-672,-672).
故答案为:(0,671
| 3 |
点评:本题是点的变化规律的考查,主要利用了等边三角形的性质,确定出点A2013和A2014所在三角形是解题的关键.

练习册系列答案
相关题目
 如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D.
如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D. 如图,某水库堤坝横断面迎水坡AB的坡比(也叫坡度)是1:
如图,某水库堤坝横断面迎水坡AB的坡比(也叫坡度)是1: 如图,直线AB交双曲线y=
如图,直线AB交双曲线y=