Question

14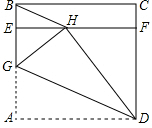．如图，ABCD是一张边长为4cm的正方形纸片，E、F分别为AB、CD上的点，且BE=CF，连接EF，沿过点D的直线将∠A翻折，使得点A落在EF上的点H处，折痕交AE于点G，当BH最短时，EG=4-4$\sqrt{2}$cm．

Answer 1

分析 根据BH+DH≥BD，DH=DA=4，所以当B、H、D在同一直线上BH最小，即H在对角线BD上，由DG平分∠ADB，所以$\frac{AG}{BG}=\frac{AD}{BD}$=$\frac{4}{4\sqrt{2}}$=$\frac{1}{\sqrt{2}}$，解得AG=4÷（1+$\sqrt{2}$）=4$\sqrt{2}$-4，则∠A=∠DHG=90°，∠ADH=45°，得到∠AGH=135°，所以∠EGH=45°，得到△EGH是等腰直角三角形，则EG=GH÷$\sqrt{2}$=AG÷$\sqrt{2}$=（4$\sqrt{2}$-4）=4-2$\sqrt{2}$．

解答 解：∵BH+DH≥BD，DH=DA=4，
∴当B、H、D在同一直线上BH最小，
即H在对角线BD上，
在Rt△ABD中，BD=$\sqrt{A{B}^{2}+A{D}^{2}}=\sqrt{{4}^{2}+{4}^{2}}=4\sqrt{2}$，
又∠GDA=∠GDH，
∴DG平分∠ADB，
∴$\frac{AG}{BG}=\frac{AD}{BD}$=$\frac{4}{4\sqrt{2}}$=$\frac{1}{\sqrt{2}}$，
∴$\frac{AG}{4-AG}=\frac{1}{\sqrt{2}}$
AG=4÷（1+$\sqrt{2}$）=4$\sqrt{2}$-4，
则∠A=∠DHG=90°，∠ADH=45°，
∴∠AGH=135°，
∴∠EGH=45°，
∴△EGH是等腰直角三角形，
∴EG=GH÷$\sqrt{2}$=AG÷$\sqrt{2}$=（4$\sqrt{2}$-4）÷$\sqrt{2}$=4-2$\sqrt{2}$．
故答案为：4-2$\sqrt{2}$．

点评 本题考查了正方形的性质、图形的翻折问题、角平分线的性质，解决本题的关键是当B、H、C在同一直线上BH最小，即H在对角线BD上．