Question

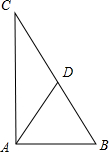如图，直角△ABC中，∠BAC=90°，D是BC边上的中点，已知sin∠C=

5

13

，AC=12．
（1）求BC的长；
（2）求sin∠ADB的值．

Answer 1

考点：解直角三角形,直角三角形斜边上的中线

专题：

分析：（1）先在直角△ABC中，由sin∠C=

5

13

，根据正弦函数的定义可设AB=5k，则BC=13k，由勾股定理求出AC=

BC2-AB2

=12k，而AC=12，那么k=1，于是求出AB=5，BC=13；
（2）先根据直角三角形斜边上的中线等于斜边的一半得出AD=

1

2

BC=

13

2

，再过A作AE⊥BC于E．根据S_△ABC=

1

2

BC•AE=

1

2

AB•AC，求出AE=

60

13

，然后在直角△ADE中利用正弦函数的定义即可求出sin∠ADB的值．

解答：解：（1）直角△ABC中，∵∠BAC=90°，sin∠C=

5

13

，
∴

AB

BC

=

5

13

，
设AB=5k，则BC=13k，
由勾股定理得，AC=

BC2-AB2

=12k，
∵AC=12，
∴12k=12，
∴k=1，
∴AB=5，BC=13；

（2）∵直角△ABC中，∠BAC=90°，D是BC边上的中点，
∴AD=

1

2

BC=

13

2

．
过A作AE⊥BC于E．
∵S_△ABC=

1

2

BC•AE=

1

2

AB•AC，
∴AE=

AB•AC

BC

=

5×12

13

=

60

13

，
∴sin∠ADB=

AE

AD

=

60 13

13 2

=

120

169

．

点评：本题考查了解直角三角形，锐角三角函数的定义，勾股定理，直角三角形斜边上的中线等于斜边的一半的性质，三角形的面积，难度适中．（2）中准确作出辅助线求出AE的长是解题的关键．