题目内容
17.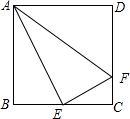 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD.
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD.(1)设AB=4m,用含m的代数式表示AE和EF的长;
(2)求证:∠AEB=∠EFC.
分析 (1)根据已知条件得到BE=$\frac{1}{2}$BC=$\frac{1}{2}$AB=2m,由勾股定理得到AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{(4m)^{2}+(2m)^{2}}$=2$\sqrt{5}$m2,通过△ABE∽△CEF,根据相似三角形的性质得到$\frac{AB}{CE}=\frac{AE}{EF}$,代入数据即可得到结论;
(2)根据相似三角形的性质即可得到结论.
解答 解:(1)∵在正方形ABCD中,E是BC的中点,
∴BE=$\frac{1}{2}$BC=$\frac{1}{2}$AB=2m,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{(4m)^{2}+(2m)^{2}}$=2$\sqrt{5}$m2,
∵$\frac{CE}{AB}=\frac{1}{2}$,
∵CF=$\frac{1}{4}$CD,
∴CF=$\frac{1}{4}$•4m=m,
∴$\frac{CF}{BE}=\frac{m}{2m}$=$\frac{1}{2}$,
∴$\frac{CE}{AB}=\frac{CF}{BE}$,
∵∠B=∠C=90°,
∴△ABE∽△CEF,
∴$\frac{AB}{CE}=\frac{AE}{EF}$,
∴$\frac{4m}{2m}=\frac{2\sqrt{5}m}{EF}$,
∴EF=$\sqrt{5}$m;
(2)∵△ABE∽△CEF,
∴∠AEB=∠EFC.
点评 不要看错了相似三角形的判定和性质,正方形的性质,勾股定理,熟练掌握相似三角形的性质是解题的关键.

练习册系列答案
相关题目
2.已知正n边形的半径为R,边长为a,若a=$\sqrt{3}$R,则n等于( )
| A. | 3 | B. | 4 | C. | 6 | D. | 12 |
 如图,⊙O为Rt△ABC的内切圆,切点为D、E、F,半径为r,∠C=90°,AB、BC、AC的长为c、a、b,求r.
如图,⊙O为Rt△ABC的内切圆,切点为D、E、F,半径为r,∠C=90°,AB、BC、AC的长为c、a、b,求r.
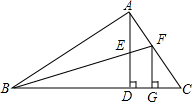 如图,已知△ABC中,∠BAC=90°,AD⊥BC于D,E是AD的中点,BE的延长线交AC于F,FG⊥BC于G.求证:$\frac{FG}{AF}$=$\frac{CF}{FG}$.
如图,已知△ABC中,∠BAC=90°,AD⊥BC于D,E是AD的中点,BE的延长线交AC于F,FG⊥BC于G.求证:$\frac{FG}{AF}$=$\frac{CF}{FG}$.