题目内容
2.已知正n边形的半径为R,边长为a,若a=$\sqrt{3}$R,则n等于( )| A. | 3 | B. | 4 | C. | 6 | D. | 12 |
分析 连接OA、OB,作OM⊥AB于M,则∠OMA=90°,由垂径定理得出AM=BM=$\frac{1}{2}$a=$\frac{\sqrt{3}}{2}$R,由三角函数求出∠AOM=60°,得出∠AOB=120°,即可得出结果.
解答 解:如图所示: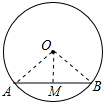
AB为正n边形的边,连接OA、OB,作OM⊥AB于M,
则∠OMA=90°,AM=BM=$\frac{1}{2}$a=$\frac{\sqrt{3}}{2}$R,
∵sin∠AOM=$\frac{AM}{OA}$=$\frac{\sqrt{3}}{2}$,
∴∠AOM=60°,
∴∠AOB=120°,
∴n=$\frac{360°}{120°}$=3.
故选:A.
点评 本题考查了正多边形的性质、三角函数、垂径定理、中心角与边数的关系;熟练掌握正多边形的性质,由三角函数求出中心角的度数是解题的关键.

练习册系列答案
相关题目
17.以下说法正确的是( )
| A. | 每个内角都是120°的六边形一定是正六边形 | |
| B. | 正n边形的对称轴不一定有n条 | |
| C. | 正n边形的每一个外角度数等于它的中心角度数 | |
| D. | 正多边形一定既是轴对称图形,又是中心对称图形 |
7.某公园的门票价格规定如下表:
某校七年级甲、乙两个班共108人去游该公园,其中甲班人数较少,不到50人,乙班人数较多,有50多人.经估算,如果两班联合起来,作为一个团体购票,则一共应付1286元,问:
(1)两班各有学生多少人?
(2)如果两班联合起来,作为一个团体购票,可以省多少钱?
| 购票人数 | 1-50人 | 51-100人 | 100人以上 |
| 每人门票价 | 13元 | 11元 | 9元 |
(1)两班各有学生多少人?
(2)如果两班联合起来,作为一个团体购票,可以省多少钱?
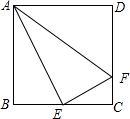 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD.
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD.