题目内容
17.某工程队修建一条长1200米的道路.工程队花费45000元购买材料用于修路,一段时间后,又花费21000元第二次购买材料.第二次购买量是第一次的一半,但单价比第一次少100元,问这两次各购买多少吨材料?分析 设第一次购进的材料单价是x元,第二次购进的材料的单价是(x-100)元,根据购买量是第一次的一半,据此列方程求解.
解答 解:设第一次购进的材料单价是x元,第二次购进的材料的单价是(x-100)元,
由题意得,$\frac{45000}{x}$=2×$\frac{21000}{x-100}$,
解得:x=625,
经检验:x=625是原分式方程的解,且符合题意.
45000÷625=72(吨),72×$\frac{1}{2}$=36(吨),
答:第一次购买72吨材料,第二次购买36吨材料.
点评 本题考查了分式方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解,注意检验.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.当m,n是实数且满足m-n=mn时,就称点Q(m,$\frac{m}{n}}$)为“奇异点”,已知点A、点B是“奇异点”且都在反比例函数y=$\frac{2}{x}$的图象上,点O是平面直角坐标系原点,则△OAB的面积为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
8.下列计算结果为正数的是( )
| A. | (-$\frac{1}{2}$)-2 | B. | -(-$\frac{1}{2}$)0 | C. | (-$\frac{1}{2}$)3 | D. | -|$\frac{1}{2}$| |
19.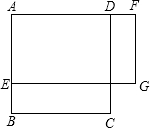 如图,正方形ABCD的边长为5,点E是AB上一点,点F是AD延长线上一点,且BE=DF.四边形AEGF是矩形,则矩形AEGF的面积y与BE的长x之间的函数关系式为( )
如图,正方形ABCD的边长为5,点E是AB上一点,点F是AD延长线上一点,且BE=DF.四边形AEGF是矩形,则矩形AEGF的面积y与BE的长x之间的函数关系式为( )
 如图,正方形ABCD的边长为5,点E是AB上一点,点F是AD延长线上一点,且BE=DF.四边形AEGF是矩形,则矩形AEGF的面积y与BE的长x之间的函数关系式为( )
如图,正方形ABCD的边长为5,点E是AB上一点,点F是AD延长线上一点,且BE=DF.四边形AEGF是矩形,则矩形AEGF的面积y与BE的长x之间的函数关系式为( )| A. | y=5-x | B. | y=5-x2 | C. | y=25-x | D. | y=25-x2 |
20. 如图,数轴上A,B两点表示的数分别为-1,-$\sqrt{2}$,点B关于点A的对称点为点C,则点C所表示的数是( )
如图,数轴上A,B两点表示的数分别为-1,-$\sqrt{2}$,点B关于点A的对称点为点C,则点C所表示的数是( )
 如图,数轴上A,B两点表示的数分别为-1,-$\sqrt{2}$,点B关于点A的对称点为点C,则点C所表示的数是( )
如图,数轴上A,B两点表示的数分别为-1,-$\sqrt{2}$,点B关于点A的对称点为点C,则点C所表示的数是( )| A. | 1-$\sqrt{2}$ | B. | $\sqrt{2}$-1 | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}$-2 |
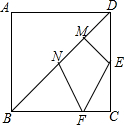 正方形ABCD,AB=4,E是CD中点,BF=3CF,点M,N为线段BD上的动点,MN=$\sqrt{2}$,求四边形EMNF周长的最小值$\sqrt{13}$+$\sqrt{2}$+$\sqrt{5}$.
正方形ABCD,AB=4,E是CD中点,BF=3CF,点M,N为线段BD上的动点,MN=$\sqrt{2}$,求四边形EMNF周长的最小值$\sqrt{13}$+$\sqrt{2}$+$\sqrt{5}$.