题目内容
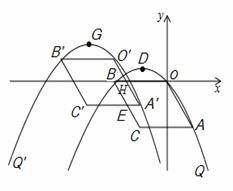
如图,在平面直角坐标系xOy中,四边形OACB是平行四边形,A、B两点的坐标分别为(2,﹣4),(﹣4,0),抛物线Q经过O、A、B三点,D是抛物线Q的顶点.
(1)求抛物线Q的解析式及顶点D的坐标;
(2)将抛物线Q和平行四边形OACB一起先向左平移4个单位后,再向上平移m(0<m<3)个 单位,得到抛物线Q′和平行四边形O′A′C′B′,在向下平移的过程中,设平行四边形O′A′C′B′与平
单位,得到抛物线Q′和平行四边形O′A′C′B′,在向下平移的过程中,设平行四边形O′A′C′B′与平 行四边形OACB的重叠部分的面积为S,试探究:当m为何值时S有最大值,并求出S的最大值;
行四边形OACB的重叠部分的面积为S,试探究:当m为何值时S有最大值,并求出S的最大值;
(3)在(2)的条件下,当S取最大值时,设此时抛物线Q′的顶点为G,若点M是x轴上的动点,点N是抛物线Q′上的动点,试判断是否存在这样的点M和点N,使得以D、G、M、N为顶点的四边形是平行四边形?若存在,请求出点所有的M的坐标;若不存在,请说明理由.
(1) D(-2,
D(-2, )
)
(2)
(3)抛物线Q’的解析式为 ,G点(-6,
,G点(-6, )
)
当N点在x轴上方时,N点(-8,2)或(-4,2) M点(-4 ,0)或(0,0)
,0)或(0,0)
当N点在x轴下方时,N点(-10,-2)或(-2,-2) M点(-14,0)或(-6,0)
故M点坐标为(-4,0),(0,0), (-14,0)或(-6,0)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 的自变量
的自变量 的取值范围是 .
的取值范围是 .
 ,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )
,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )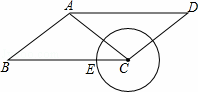
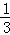 ,则黄球的个数为( )
,则黄球的个数为( )