题目内容
6．解方程组$\left\{\begin{array}{l}{3x+2y=1①}\\{2x-y+2z=-7②}\\{x+2y-z=3③}\end{array}\right.$．分析 由方程②、③可消去z，再与方程①组成二元一次方程组求解即可．
解答 解：
②+2×③可得：4x+3y=-1④，
由①、④组成二元一次方程组$\left\{\begin{array}{l}{3x+2y=1①}\\{4x+3y=-1④}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x=5}\\{y=-7}\end{array}\right.$，代入③可得5-14-z=3，解得z=-12，
∴原方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=-7}\\{z=-12}\end{array}\right.$．
点评 本题主要考查三元一次方程组的解法，解方程组即“转化”，化高次为低次，注意消元的方法．
练习册系列答案
相关题目
为了美化环境，某学校在教学楼前铺设小广场地面，其图案如图所示，正方形小广场地面的边长是40米．中心建一个直径为正方形边长一半的圆形花坛，四个角各留一个边长为正方形小广场的四分之一的小正方形花坛，种植高大的树木．图中阴影郁分铺设广场砖．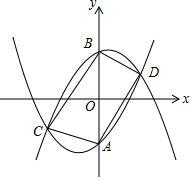
在平面直角坐标系中，我们把关于原点对称的两条抛物线叫做“哥俩好”抛物线．