题目内容
19.如图(1),在Rt△ABC中,∠ACB=90°D为斜边AB的中点,动点P从B点出发,沿B→C→A运动,设S△DPB=y,点P运动的路程为x,若y与x之间的函数图象如图(2)所示,则AB的长为5.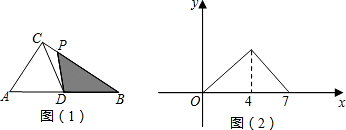
分析 根据题意可以得到BC和AC的长,由∠ACB=90°,根据勾股定理可以求得AB的长,本题得以解决.
解答 解:由题意可知,
当点P从点B运动到点C时,面积达到最大,当运动到点A时,面积变为0,
由图(2)可知,BC=4,CA=7-4=3,
∵∠ACB=90°,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}=\sqrt{{4}^{2}+{3}^{2}}=5$,
故答案为:5.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,利用数形结合的思想解答问题.

练习册系列答案
相关题目
14.圆锥体是由下列哪个图形绕自身的对称轴旋转一周得到的( )
| A. | 正方形 | B. | 等腰三角形 | C. | 圆 | D. | 等腰梯形 |
 如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=2,则弦BC=2$\sqrt{3}$.
如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=2,则弦BC=2$\sqrt{3}$. 如图,在正方形ABCD中,将△ABP绕B点顺时针旋转,能与△CBP′重合,若BP=a,则PP′=$\sqrt{2}$a.
如图,在正方形ABCD中,将△ABP绕B点顺时针旋转,能与△CBP′重合,若BP=a,则PP′=$\sqrt{2}$a.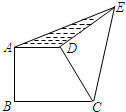 如图,直角梯形ABCD中,AD∥BC,AB⊥BC,∠BCD=45°,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是1.
如图,直角梯形ABCD中,AD∥BC,AB⊥BC,∠BCD=45°,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是1.