题目内容
7.已知实数对(x,y)满足方程(x-2)2+y2=3,记$\frac{y}{x}$的最小值,最大值分别为a,b,则a2+b2=6.分析 设$\frac{y}{x}$=t,则y=tx,则得到关于x的一元二次方程(1+t2)x2-4x+1=0,利用判别式的意义得到t2≤3,解得-$\sqrt{3}$≤t≤$\sqrt{3}$,于是得到a=-$\sqrt{3}$,b=$\sqrt{3}$,然后计算a2+b2的值.
解答 解:设$\frac{y}{x}$=t,则y=tx,
∵(x-2)2+y2=3,
∴x2-4x+4+t2x2=3,
即(1+t2)x2-4x+1=0,
△=16-4(1+t2)≥0,
化简得t2≤3,
∴-$\sqrt{3}$≤t≤$\sqrt{3}$,
∴a=-$\sqrt{3}$,b=$\sqrt{3}$,
∴a2+b2=3+3=6.
故答案为6.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
17.三元一次方程组$\left\{\begin{array}{l}{x+y=1}\\{y+z=5}\\{z+x=6}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=0}\\{z=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=0}\\{z=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=1}\\{z=0}\end{array}\right.$ |
 如图,已知:∠1=∠2,AC=AE,BC=DE,且点D在BC上,求证:AB=AD.
如图,已知:∠1=∠2,AC=AE,BC=DE,且点D在BC上,求证:AB=AD. 如图,点(3,m)为直线AB上的点.求该点的坐标.
如图,点(3,m)为直线AB上的点.求该点的坐标. 对于平面直角坐标系中的线段PQ和点M,在△MPQ中,当PQ边上的高为2时,称M为PQ的“等高点”,称此时MP+MQ为PQ的“等高距离”.己知P(1,2),Q(4,2).
对于平面直角坐标系中的线段PQ和点M,在△MPQ中,当PQ边上的高为2时,称M为PQ的“等高点”,称此时MP+MQ为PQ的“等高距离”.己知P(1,2),Q(4,2).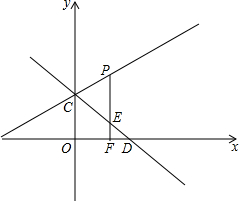 如图,直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D,点P是直线y=$\frac{1}{2}$x+3上的一个动点(点P在第一象限),过P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.
如图,直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D,点P是直线y=$\frac{1}{2}$x+3上的一个动点(点P在第一象限),过P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.