题目内容
若x+y=4，xy=3，求①（x-y）2；②x2y+xy2的值．
考点：因式分解的应用
专题：
分析：①转换成（x+y）2-4xy，②因式分解可得xy（x+y），再代入计算即可．
解答：解：∵x+y=4，xy=3，
∴①（x-y）2=（x+y）2-4xy=42-4×3=16-12=4，
②x2y+xy2=xy（x+y）=3×4=12．
∴①（x-y）2=（x+y）2-4xy=42-4×3=16-12=4，
②x2y+xy2=xy（x+y）=3×4=12．
点评：本题主要考查因式分解的应用，利用因式分解把所求代数式化为关于x+y和xy的式子是解题的关键．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
若
=
，则
=（ ）
| a |
| b |
| 2 |
| 3 |
| a+2b |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，△ABD≌△CBD，若∠A=80°，∠ABC=70°，则∠BDC的度数为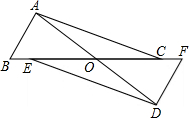
已知，如图，AD、BF相交于O点，点E、C在BF上，且BE=FC，AC=DE，AB=DF．求证：