题目内容
9. 如图,如果?ABCD的内角∠BAD的平分线交BC于点E,且AE=BE,
如图,如果?ABCD的内角∠BAD的平分线交BC于点E,且AE=BE,(1)求?ABCD各内角的度数;
(2)若AB=4,AD=5,求?ABCD的面积.
分析 (1)证明△ABE是等边三角形即可解决问题.
(2)作AH⊥BE于H,根据平行四边形ABCD的面积=AD×AH,求出AH即可解决问题.
解答 (1)解:∵四边形ABCD是平行四边形, ∴AD∥BC,∠B=∠D,∠C=∠BAD,
∴AD∥BC,∠B=∠D,∠C=∠BAD,
∵EA平分∠BAD,
∴∠BAE=∠DAE=∠AEB,
∵AE=BE,
∴∠EAB=∠B=∠AEB,
∴△ABE是等边三角形,
∴∠B=∠D=60°,∠C=∠BAD=120°.
(2)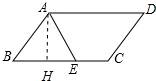 作AH⊥BE于H,
作AH⊥BE于H,
由(1)可知,△ABE是等边三角形,
∴AH=$\frac{\sqrt{3}}{2}$×4=2$\sqrt{3}$,
∴平行四边形ABCD的面积=AD×AH=10$\sqrt{3}$.
点评 本题考查平行四边形的性质、等边三角形的判定和性质等知识,解题的关键是灵活应用这些知识解决问题,属于中考常考题型.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
19.方程4-2x=0的解是( )
| A. | x=2 | B. | x=-2 | C. | x=$\frac{1}{2}$ | D. | x=-$\frac{1}{2}$ |
20.某蔬菜公司收购某种蔬菜140t,准备加工上市销售.该公司加工能力是:每天可以精加工6t或粗加工16t.必须在15天内完成加工任务.设精加工x天,粗加工y天,可得方程组( )
| A. | $\left\{\begin{array}{l}{x+y=140}\\{16x+6y=15}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=15}\\{16x+6y=140}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=140}\\{6x+16y=15}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=15}\\{6x+16y=140}\end{array}\right.$ |
17.将方程x2+4x+3=0配方后,原方程变形为( )
| A. | (x+2)2=1 | B. | (x+4)2=1 | C. | (x+2)2=-3 | D. | (x+2)2=-1 |
19.计算3.8×10-7-3.7×10-7,结果用科学记数法表示为( )
| A. | 0.1×10-7 | B. | 1×10-6 | C. | 0.1×10-8 | D. | 1×10-8 |
 如图,在平行四边形ABCD中,E、F为对角线BD上两点,且满足BF=DE,连接AE、CE、AF、CF.求证:四边形AECF为平行四边形.
如图,在平行四边形ABCD中,E、F为对角线BD上两点,且满足BF=DE,连接AE、CE、AF、CF.求证:四边形AECF为平行四边形.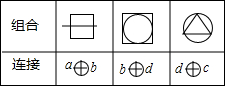 字母a,b,c,d各代表正方形、线段、正三角形、圆四个图形中的一种,将它们两两组合,并用字母连接表示,如表是三种组合与连接的对应表,由此可推断图形
字母a,b,c,d各代表正方形、线段、正三角形、圆四个图形中的一种,将它们两两组合,并用字母连接表示,如表是三种组合与连接的对应表,由此可推断图形 的连接方式为a⊕c.
的连接方式为a⊕c.