题目内容
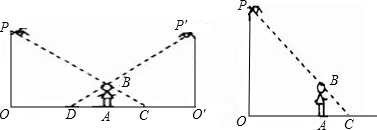
如图，李华晚上在路灯下散步．已知李华的身高AB=h，灯柱的高OP=O′P′=l，两灯柱之间的距离OO′=m．（1）若李华距灯柱OP的水平距离OA=a，求他影子AC的长；
（2）若李华在两路灯之间行走，则他前后的两个影子的长度之和（DA+AC）是否是定值请说明理由；
（3）若李华在点A朝着影子（如图箭头）的方向以v1匀速行走，试求他影子的顶端在地面上移动的速度v2．
分析：利用相似三角形对应边成比例解题．
解答：解：（1）由题意可知：AB∥OP，
∴△ABC∽△OPC．
∴
=
，
∵OP=l，AB=h，OA=a，
∴
=
，
∴解得：AC=
．
（2）∵AB∥OP，
∴△ABC∽△OPC，
∴
=
=
，
即
=
，即
=
．
∴AC=
•OA．
同理可得：DA=
•O′A，
∴DA+AC=
(OA+O′A)=
是定值．
（3）根据题意设李华由A到A'，身高为A'B'，A'C'代表其影长（如图）．
由（1）可知
=
，即
=
，∴
=
=
，
同理可得：
=
，
∴
=
，
由等比性质得：
=
=
，
当李华从A走到A'的时候，他的影子也从C移到C'，因此速度与路程成正比
∴
=
=
，
所以人影顶端在地面上移动的速度为v2=
．
∴△ABC∽△OPC．
∴
| AC |
| OC |
| AB |
| OP |
∵OP=l，AB=h，OA=a，
∴
| AC |
| a+AC |
| h |
| l |
∴解得：AC=
| ah |
| l-h |
（2）∵AB∥OP，
∴△ABC∽△OPC，
∴
| AB |
| OP |
| AC |
| OC |
| h |
| l |
即
| AC |
| OC-AC |
| h |
| l-h |
| AC |
| OA |
| h |
| l-h |
∴AC=
| h |
| l-h |
同理可得：DA=
| h |
| l-h |
∴DA+AC=
| h |
| l-h |
| hm |
| l-h |
（3）根据题意设李华由A到A'，身高为A'B'，A'C'代表其影长（如图）．由（1）可知
| AC |
| OC |
| AB |
| OP |
| h |
| l |
| AC |
| OC |
| OA |
| OC |
| OC-AC |
| OC |
| l-h |
| l |
同理可得：
| OA′ |
| OC′ |
| l-h |
| l |
∴
| OA |
| OC |
| OA′ |
| OC′ |
由等比性质得：
| AA′ |
| CC′ |
| OA′-OA |
| OC′-OC |
| l-h |
| l |
当李华从A走到A'的时候，他的影子也从C移到C'，因此速度与路程成正比
∴
| AA′ |
| CC′ |
| v1 |
| v2 |
| l-h |
| l |
所以人影顶端在地面上移动的速度为v2=
| lv1 |
| l-h |
点评：此题是把实际问题转化成相似三角形的问题，然后利用相似三角形对应边成比例解题．
练习册系列答案
相关题目
如图，李华晚上在路灯下散步．已知李华的身高AB=h，灯柱的高OP=O′P′=l，两灯柱之间的距离OO′=m．若李华距灯柱OP的水平距离OA=a，求他影子AC的长．
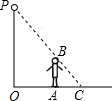如图，李华晚上在路灯下散步，已知李华的身高AB=h，灯柱的高OP=l，李华距灯柱OP的水平距离OA=a．
如图，李华晚上在路灯下散步．已知李华的身高AB=h，灯柱的高OP=l，若李华在点A朝着影子的方向以v1匀速行走，则他影子的顶端在地面上移动的速度v2为