题目内容
 角平分尺是用来平分一个角的,某同学如图,在制作角平分尺时,保证AB=AC,BD=CD.AD是用一根具有弹性的皮筋连接.
角平分尺是用来平分一个角的,某同学如图,在制作角平分尺时,保证AB=AC,BD=CD.AD是用一根具有弹性的皮筋连接.(1)尝试说明这位同学设计的可行性;
提示:∠A可否改变大小,依据是什么?
(2)若可行,证明AD平分∠BAC.
考点:线段垂直平分线的性质,等腰三角形的性质
专题:
分析:(1)∠A可改变大小,依据是线段垂直平分线的性质与等腰三角形的性质;
(2)由AB=AC,BD=CD,根据线段垂直平分线的性质,可得AD是BC的垂直平分线,然后由三线合一的性质,证得AD平分∠BAC.
(2)由AB=AC,BD=CD,根据线段垂直平分线的性质,可得AD是BC的垂直平分线,然后由三线合一的性质,证得AD平分∠BAC.
解答: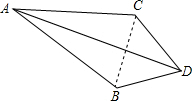 解:(1)∠A可改变大小,依据是线段垂直平分线的性质与等腰三角形的性质;
解:(1)∠A可改变大小,依据是线段垂直平分线的性质与等腰三角形的性质;
(2)连接BC,
∵AB=AC,BD=CD,
∴点A在BC的垂直平分线上,点D在BC的垂直平分线上,
∴AD是BC的垂直平分线,
∴AD平分∠BAC.
 解:(1)∠A可改变大小,依据是线段垂直平分线的性质与等腰三角形的性质;
解:(1)∠A可改变大小,依据是线段垂直平分线的性质与等腰三角形的性质;(2)连接BC,
∵AB=AC,BD=CD,
∴点A在BC的垂直平分线上,点D在BC的垂直平分线上,
∴AD是BC的垂直平分线,
∴AD平分∠BAC.
点评:此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
(a+2b)2-(x-3y)2分解因式为( )
| A、(a+2b+x-3y)(a+2b-x-3y) |
| B、(a+2b+x-3y)(a+2b-x+3y) |
| C、(a+2b+x+3y)(a+2b-x-3y) |
| D、(a+2b+x+3y)(a+2b-x+3y) |
 如图,△ACB≌△A′CB′,∠BCB′=35°,则∠ACA′的度数为( )
如图,△ACB≌△A′CB′,∠BCB′=35°,则∠ACA′的度数为( )| A、35° | B、40° |
| C、45° | D、50° |
已知等腰三角形的一个外角等于110°,则它的顶角度数是( )度.
| A、40 | B、70 |
| C、40或70 | D、140 |
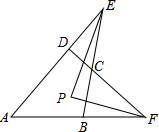 四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=44°,∠BCD=136°.
四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=44°,∠BCD=136°.