题目内容
15.边长分别为3、4、5的三角形的内心到一边的距离是1.分析 首先证明△ABC是直角三角形,再利用$\frac{1}{2}$•AB•r+$\frac{1}{2}$•BC•r+$\frac{1}{2}$•AC•r=$\frac{1}{2}$•BC•AC即可解决.
解答 解:如图,⊙O是△ABC的内切圆,切点分别为E、F、G.
∵AB=5,AC=3,BC=4,
∴AC2+BC2=AB2,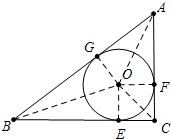
∴∠ACB=90°,
设OG=OE=OF=r,
∵$\frac{1}{2}$•AB•r+$\frac{1}{2}$•BC•r+$\frac{1}{2}$•AC•r=$\frac{1}{2}$•BC•AC,
∴5r+4r+3r=12,
∴r=1.
故答案为1.
点评 本题考查三角形内心、勾股定理的逆定理,解题关键是判断三角形是直角三角形,学会用面积法求内切圆半径,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 如图,已知点D是△ABC的重心,连接BD并延长,交AC于点E,若AE=4,则AC的长度为( )
如图,已知点D是△ABC的重心,连接BD并延长,交AC于点E,若AE=4,则AC的长度为( )
 如图,已知点D是△ABC的重心,连接BD并延长,交AC于点E,若AE=4,则AC的长度为( )
如图,已知点D是△ABC的重心,连接BD并延长,交AC于点E,若AE=4,则AC的长度为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
5.下列语句中错误的是( )
| A. | 若旋转对称图形的旋转角为180°,那么这个图形也是中心对称图形 | |
| B. | 轴对称图形中,对应点的连线被对称轴垂直平分 | |
| C. | 图形平移后,对应点的连线相互平行或重合 | |
| D. | 中心对称图形的对应点连线交于一点,这点就是对称中心 |
 在平面直角坐标系中,描出点A(0,2),B(-1,0),过点A作直线l1∥x轴,过点B作l2∥y轴,分析l1,l2上点的坐标特点.由此,你能总结出什么规律?
在平面直角坐标系中,描出点A(0,2),B(-1,0),过点A作直线l1∥x轴,过点B作l2∥y轴,分析l1,l2上点的坐标特点.由此,你能总结出什么规律? 如图,这是某邮递员投递区域街道图,现在,他要把一封电报从邮政局所在的O地尽快到A地,他所走的一条路线可用(0,0)→(0,3)→(4,3)→(4,8)→(7,8)表示,请你用这种形式出由O地到A地的其他几条路线.
如图,这是某邮递员投递区域街道图,现在,他要把一封电报从邮政局所在的O地尽快到A地,他所走的一条路线可用(0,0)→(0,3)→(4,3)→(4,8)→(7,8)表示,请你用这种形式出由O地到A地的其他几条路线.