题目内容
2.计算(1)2$\sqrt{3}+3\sqrt{12}-\sqrt{48}$
(2)(2$\sqrt{3}$-$\sqrt{54}$)$\sqrt{6}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先把各二次根式化为最简二次根式,然后进行二次根式的乘法运算.
解答 解:(1)原式=2$\sqrt{3}$+6$\sqrt{3}$-4$\sqrt{3}$
=4$\sqrt{3}$;
(2)原式=2$\sqrt{3}$•$\sqrt{6}$-3$\sqrt{6}$•$\sqrt{6}$
=6$\sqrt{2}$-18.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.若反比例函数y=$\frac{m}{x}$的图象经过点(3,-2),那么这个函数的表达式为( )
| A. | y=-6x | B. | y=-$\frac{6}{x}$ | C. | y=6x | D. | y=$\frac{1}{-6x}$ |
12.根据下列条件,能判定平行四边形ABCD是矩形的是( )
| A. | AB=CD,AD=BC | B. | AB=BC | C. | AC=BD | D. | AB∥CD,AD∥BC |
 如图,∠1=∠ABC,∠2+∠D=180°,EF与CD平行吗?AB与CD平行吗?说明理由.
如图,∠1=∠ABC,∠2+∠D=180°,EF与CD平行吗?AB与CD平行吗?说明理由.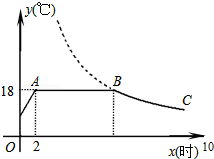 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.下图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=$\frac{k}{x}$的一部分.请根据图中信息解答下列问题:
我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.下图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=$\frac{k}{x}$的一部分.请根据图中信息解答下列问题: