题目内容
在Rt△ACB中,∠C=90°,tanB=
,则cosA=( )
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:互余两角三角函数的关系
专题:
分析:根据互为余角两角的关系:可得cotA,根据同角三角函数值,可得答案.
解答:解:由在Rt△ACB中,∠C=90°,tanB=
,得
cotA=
=
,sinA=3cosA.
由sin2A+cos2A=1,得
10cos2A=1,
解得cosA=
,cosA=-
(不符合题意要舍去),
故选:D.
| 1 |
| 3 |
cotA=
| 1 |
| 3 |
| cosA |
| sinA |
由sin2A+cos2A=1,得
10cos2A=1,
解得cosA=
| ||
| 10 |
| ||
| 10 |
故选:D.
点评:本题考查了互余两角三角函数关系,利用了互为余角的两个三角函数:一个角的正切等于它余角的余切.

练习册系列答案
相关题目
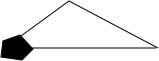 如图所示,八年级某同学书上的图形(三角形)不小心被墨迹污染了一部分,但他很快就根据所学知识,画出一个与书上完全一样的三角形,那么这两个三角形全等的依据是( )
如图所示,八年级某同学书上的图形(三角形)不小心被墨迹污染了一部分,但他很快就根据所学知识,画出一个与书上完全一样的三角形,那么这两个三角形全等的依据是( )| A、SSS | B、SAS |
| C、ASA | D、AAS |
在一个不透明的口袋里装了一些红球和白球,每个球除颜色外都相同.将球摇匀,从中任意摸出一个球,则摸到白球是( )
| A、必然事件 | B、不可能事件 |
| C、随机事件 | D、确定事件 |