题目内容
10.一组数据1、3、5、7的方差是5.分析 先求出这组数据的平均数,再根据方差公式S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],进行计算即可.
解答 解:数据的平均数$\overline{x}$=$\frac{1}{4}$(1+3+5+7)=4,
方差s2=$\frac{1}{4}$[(1-4)2+(3-4)2+(5-4)2+(7-4)2]=5.
则一组数据1、3、5、7的方差是5.
故答案为:5.
点评 本题考查了方差的定义,一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18. 如图,将长方形纸片ABCD的角C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若FH平分∠BFE,则∠GFH的度数( )
如图,将长方形纸片ABCD的角C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若FH平分∠BFE,则∠GFH的度数( )
 如图,将长方形纸片ABCD的角C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若FH平分∠BFE,则∠GFH的度数( )
如图,将长方形纸片ABCD的角C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若FH平分∠BFE,则∠GFH的度数( )| A. | 大于90° | B. | 小于90° | ||
| C. | 等于90° | D. | 随折痕GF位置的变化而变化 |
2.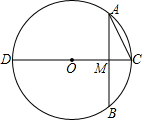 如图,已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长度为( )
如图,已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长度为( )
 如图,已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长度为( )
如图,已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长度为( )| A. | 4$\sqrt{5}$cm | B. | 3$\sqrt{5}$cm | C. | 2$\sqrt{5}$cm | D. | $\sqrt{5}$cm |
 如图,一建筑物AB(看做线段)在阳光下的投影为BC,小红站在BC上,现她不想看到自己的影子,请你在图上画出她的活动范围.
如图,一建筑物AB(看做线段)在阳光下的投影为BC,小红站在BC上,现她不想看到自己的影子,请你在图上画出她的活动范围. 如图,反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b图象的交点为A(m,1),B(-2,n),OA与x轴正方向的夹角为α,且tanα=$\frac{1}{4}$.
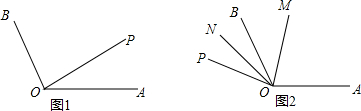
如图,反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b图象的交点为A(m,1),B(-2,n),OA与x轴正方向的夹角为α,且tanα=$\frac{1}{4}$. 如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠AOB等于100°.
如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠AOB等于100°. 反比例函数y=$\frac{k}{x}$的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=3,那么k的值是-6.
反比例函数y=$\frac{k}{x}$的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=3,那么k的值是-6.