题目内容
12．计算：2008$\frac{1}{18}$+2009$\frac{1}{54}$+2010$\frac{1}{108}$+2011$\frac{1}{180}$+2012$\frac{1}{270}$=10050$\frac{5}{54}$．分析 利用加法交换律，将同类型的数各自相加．
解答 解：原式=（2008+2009+2010+2011+2012）+（$\frac{1}{18}$+$\frac{1}{54}$+$\frac{1}{108}$+$\frac{1}{180}$+$\frac{1}{270}$）
=10050+$\frac{1}{18}$×（1+$\frac{1}{3}$+$\frac{1}{6}$+$\frac{1}{10}$+$\frac{1}{15}$）
=10050+$\frac{1}{18}$×$\frac{5}{3}$
=10050$\frac{5}{54}$
故答案为：10050$\frac{5}{54}$．
点评 本题主要考查有理数的加法，根据式子中各数的特点选择合适、简便的方法是关键．
练习册系列答案
相关题目
20．
如图，已知l1∥l2∥l3，下列比例式中成立的是（ ）
如图，已知l1∥l2∥l3，下列比例式中成立的是（ ）| A． | $\frac{AD}{DF}$=$\frac{CE}{BC}$ | B． | $\frac{AD}{BE}$=$\frac{BC}{AF}$ | C． | $\frac{CE}{DF}$=$\frac{AD}{BC}$ | D． | $\frac{AF}{DF}$=$\frac{BE}{CE}$ |
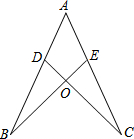如图，已知：AB=AC，AE=AD，求证：OB=OC．